K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 6 2023
a: =>2x^2-2x+2x-2-2x^2-x-4x-2=0
=>-5x-4=0
=>x=-4/5
b: =>6x^2-9x+2x-3-6x^2-12x=16
=>-19x=19
=>x=-1
c: =>48x^2-12x-20x+5+3x-48x^2-7+112x=81
=>83x=83
=>x=1
HN
5
AH
2 tháng 11 2018
a) \(3x^2--6x=0\Rightarrow3x^2+6x=0\Rightarrow3x\left(x+2\right)=0\Rightarrow\orbr{\begin{cases}3x=0\\x+2=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\x=-2\end{cases}}}\)
b) \(\left(2x-1\right)^2-16=0\Rightarrow\left(2x-1\right)^2=16\Rightarrow\orbr{\begin{cases}2x-1=4\\2x-1=-4\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{5}{2}\\x=-\frac{3}{2}\end{cases}}}\)
N
2 tháng 11 2018
\(3x^2-6x=0\)
\(\Rightarrow3x.\left(x-6\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x=0\\x-6=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=6\end{cases}}\)
\(\left(2x-1\right)^2-16=0\)
\(\left(2x-1\right)^2=16=4^2=\left(-4\right)^2\)
\(\Rightarrow\orbr{\begin{cases}2x-1=4\\2x-1=-4\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{5}{2}\\x=-\frac{3}{2}\end{cases}}\)
vậy....
PT
1
13 tháng 9 2020
a) x4 - 16x2 = 0
<=> ( x2 )2 - ( 4x )2 = 0
<=> ( x2 - 4x )( x2 + 4x ) = 0
<=> [ x( x - 4 ) ][ x( x + 4 ) ] = 0
<=> x( x - 4 )x( x + 4 ) = 0
<=> x2( x - 4 )( x + 4 ) = 0
<=> \(\hept{\begin{cases}x^2=0\\x-4=0\\x+4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm4\end{cases}}\)( thay bằng dấu hoặc hộ mình nhé )
b) 9x2 + 6x + 1 = 0
<=> ( 3x )2 + 2.3x.1 + 12 = 0
<=> ( 3x + 1 )2 = 0
<=> 3x + 1 = 0
<=> 3x = -1
<=> x = -1/3
c) x2 - 6x = 16
<=> x2 - 6x - 16 = 0
<=> x2 + 2x - 8x - 16 = 0
<=> x( x + 2 ) - 8( x + 2 ) = 0
<=> ( x + 2 )( x - 8 ) = 0
<=> \(\orbr{\begin{cases}x+2=0\\x-8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=8\end{cases}}\)
d) 9x2 + 6x = 80
<=> 9x2 + 6x - 80 = 0
<=> 9x2 + 30x - 24x - 80 = 0
<=> 9x( x + 10/3 ) - 24( x + 10/3 ) = 0
<=> ( x + 10/3 )( 9x - 24 ) = 0
<=> \(\orbr{\begin{cases}x+\frac{10}{3}=0\\9x-24=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{10}{3}\\x=\frac{8}{3}\end{cases}}\)
e) Áp dụng công thức an.bn = ( ab )n ta có :
25( 2x - 1 )2 - 9( x + 1 )2 = 0
<=> 52( 2x - 1 )2 - 32( x + 1 )2 = 0
<=> [ 5( 2x - 1 ) ]2 - [ 3( x + 1 ) ]2 = 0
<=> ( 10x - 5 )2 - ( 3x + 3 )2 = 0
<=> [ ( 10x - 5 ) - ( 3x + 3 ) ][ ( 10x - 5 ) + ( 3x + 3 ) ] = 0
<=> ( 10x - 5 - 3x - 3 )( 10x - 5 + 3x + 3 ) = 0
<=> ( 7x - 8 )( 13x - 2 ) = 0
<=> \(\orbr{\begin{cases}7x-8=0\\13x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{8}{7}\\x=\frac{2}{13}\end{cases}}\)
B
16 tháng 9 2020
Bài làm :
a) x4 - 16x2 = 0
<=> ( x2 )2 - ( 4x )2 = 0
<=> ( x2 - 4x )( x2 + 4x ) = 0
<=> [ x( x - 4 ) ][ x( x + 4 ) ] = 0
<=> x( x - 4 )x( x + 4 ) = 0
<=> x2( x - 4 )( x + 4 ) = 0
Vậy x=0 hoặc x=±4
b) 9x2 + 6x + 1 = 0
<=> ( 3x )2 + 2.3x.1 + 12 = 0
<=> ( 3x + 1 )2 = 0
<=> 3x + 1 = 0
<=> 3x = -1
<=> x = -1/3
c) x2 - 6x = 16
<=> x2 - 6x - 16 = 0
<=> x2 + 2x - 8x - 16 = 0
<=> x( x + 2 ) - 8( x + 2 ) = 0
<=> ( x + 2 )( x - 8 ) = 0
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\x-8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=8\end{cases}}\)
d) 9x2 + 6x = 80
<=> 9x2 + 6x - 80 = 0
<=> 9x2 + 30x - 24x - 80 = 0
<=> 9x( x + 10/3 ) - 24( x + 10/3 ) = 0
<=> ( x + 10/3 )( 9x - 24 ) = 0
\(\Leftrightarrow\orbr{\begin{cases}x+\frac{10}{3}=0\\9x-24=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{10}{3}\\x=\frac{8}{3}\end{cases}}\)
e) 25( 2x - 1 )2 - 9( x + 1 )2 = 0
<=> 52( 2x - 1 )2 - 32( x + 1 )2 = 0
<=> [ 5( 2x - 1 ) ]2 - [ 3( x + 1 ) ]2 = 0
<=> ( 10x - 5 )2 - ( 3x + 3 )2 = 0
<=> [ ( 10x - 5 ) - ( 3x + 3 ) ][ ( 10x - 5 ) + ( 3x + 3 ) ] = 0
<=> ( 10x - 5 - 3x - 3 )( 10x - 5 + 3x + 3 ) = 0
<=> ( 7x - 8 )( 13x - 2 ) = 0
\(\Leftrightarrow\orbr{\begin{cases}7x-8=0\\13x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{8}{7}\\x=\frac{2}{13}\end{cases}}\)
XO
13 tháng 9 2020
a) Ta có : x4 - 16x2 = 0
=> x4 - 8x2 - 8x2 + 64 = 64
=> x2(x2 - 8) - 8(x2 - 8) = 64
=> (x2 - 8)2 = 64
=> \(\orbr{\begin{cases}x^2-8=8\\x^2-8=-8\end{cases}}\Rightarrow\orbr{\begin{cases}x^2=16\\x^2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\pm4\\x=0\end{cases}}\Rightarrow x\in\left\{4;-4;0\right\}\)
b) Ta có 9x2 + 6x + 1 = 0
=> 9x2 + 3x + 3x + 1 = 0
=> 3x(3x + 1) + (3x + 1) = 0
=> (3x + 1)2 = 0
=> 3x + 1 = 0
=> x = -1/3
c) Ta có x2 - 6x = 16
=> x2 - 6x + 9 = 25
=> (x - 3)2 = 25
=> \(\orbr{\begin{cases}x-3=5\\x-3=-5\end{cases}}\Rightarrow\orbr{\begin{cases}x=8\\x=-2\end{cases}}\Rightarrow x\in\left\{8;-2\right\}\)
d) 9x2 + 6x = 80
=> 9x2 + 6x + 1 = 81
=> (3x + 1)2 = 81
=> \(\orbr{\begin{cases}3x+1=9\\3x+1=-9\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{8}{3}\\x=-\frac{10}{3}\end{cases}\Rightarrow x\in}\left\{\frac{8}{3};\frac{-10}{3}\right\}\)
e) 25(2x - 1)2 - 9(x + 1)2 = 0
=> [5(2x - 1)]2 - [3(x + 1)]2 = 0
=> (10x - 5)2 - (3x + 3)2 = 0
=> (10x - 5 - 3x - 3)(10x - 5 + 3x + 3) = 0
=> (7x - 8)(13x - 2) = 0
=> \(\orbr{\begin{cases}7x=8\\13x=2\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{8}{7}\\x=\frac{2}{13}\end{cases}}\)
ZT
2
27 tháng 10 2020
a) 6x3 - 24x = 0
⇔ 6x( x2 - 4 ) = 0
⇔ 6x( x - 2 )( x + 2 ) = 0
⇔ 6x = 0 hoặc x - 2 = 0 hoặc x + 2 = 0
⇔ x = 0 hoặc x = ±2
b) 2x( x - 3 ) - 4x + 12 = 0
⇔ 2x( x - 3 ) - 4( x - 3 ) = 0
⇔ ( x - 3 )( 2x - 4 ) = 0
⇔ x - 3 = 0 hoặc 2x - 4 = 0
⇔ x = 3 hoặc x = 2
c) 2( x - 2 ) = 3x2 - 6x
⇔ 2( x - 2 ) = 3x( x - 2 )
⇔ 2( x - 2 ) - 3x( x - 2 ) = 0
⇔ ( x - 2 )( 2 - 3x ) = 0
⇔ x - 2 = 0 hoặc 2 - 3x = 0
⇔ x = 2 hoặc x = 2/3
d) x2 - 6x = 16
⇔ x2 - 6x - 16 = 0
⇔ ( x2 - 6x + 9 ) - 25 = 0
⇔ ( x - 3 )2 - 52 = 0
⇔ ( x - 3 - 5 )( x - 3 + 5 ) = 0
⇔ ( x - 8 )( x + 2 ) = 0
⇔ x - 8 = 0 hoặc x + 2 = 0
⇔ x = 8 hoặc x = -2
27 tháng 10 2020
a) 6x^3-24x=0
<=>6x(x^2-4)=0
<=>6x(x-2)(x+2)=0
<=>6x=0 => x=0
x-2=0 => x=2
x+2=0 => x=-2
b) 2x(x-3)-4x+12=0
<=>2x(x-3)-(4x-12)=0
<=>2x(x-3)-4(x-3)=0
<=>(2x-4)(x-3)=0
<=>2x-4=0 => x=2
x-3=0 => x=3
c) 2(x-2)=3x^2-6x
<=>2(x-2)=3x(x-2)
<=>2=3x
<=>x=2/3
d) x2-6x=16
<=> x^2-6x+9=25
<=>(x-3)^2=25
<=> x-3=5 => x=8
x-3=-5 => x=-2
LT
3
27 tháng 7 2021
\(a,\left(x-3\right)\left(x+7\right)-\left(x+5\right)\left(x-1\right)=0\)
\(x^2-3x+7x-21-x^2-5x+x+5=0\)
\(-16=0\)
vậy pt vô nghiệm
\(b,\left(3x-1\right)\left(2x+7\right)-\left(x+1\right)\left(6x-5\right)=16\)
\(6x^2-2x+21x-7-6x^2-6x+5x+5=16\)
\(18x=18\)
\(x=1\left(TM\right)\)
26 tháng 8 2019
a) \(3x^3-6x^2=0\)
\(3x^2\left(x-2\right)=0\)
\(\orbr{\begin{cases}3x^2=0\\x-2=0\end{cases}}\)
\(\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
b) \(x\left(x-4\right)-12x+48=0\)
\(x^2-4x-12x+48=0\)
\(x^2-16x+48=0\)
\(\left(x-12\right)\left(x-4\right)=0\)
\(\orbr{\begin{cases}x-12=0\\x-4=0\end{cases}}\)
\(\orbr{\begin{cases}x=12\\x=4\end{cases}}\)
c) Viết thiếu nha :v
d) \(2x\left(x-5\right)-x\left(2x+3\right)=16\)
\(2x^2-10x-x^2-2x^2-3x=16\)
\(-13x=16\)
\(x=-\frac{16}{13}\)
e) \(\left(4x^2-1\right)-\left(x-1\right)^2=-3\)
\(4x^2-1-x^2+2x-1=-3\)
\(3x^2-2+2x=-3\)
\(3x^2-2+2x+3=0\)
\(3x^2+1+2x=0\)
Vì \(3x^2+1+2x>0\)nên:
\(x\in\varnothing\)
26 tháng 8 2019
A) 3x3 - 6x2 = 0
=> 3x2(x - 2) = 0
=> \(\orbr{\begin{cases}3x^2=0\\x-2=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
b) x(x - 4) - 12x + 48 = 0
=> x(x - 4) - 12(x - 4) = 0
=> (x - 12)(x - 4) = 0
=> \(\orbr{\begin{cases}x-12=0\\x-4=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=12\\x=4\end{cases}}\)
c) x(x - 4) - (x2 - 8) = x2 - 4x - x2 + 8 = 4x + 8
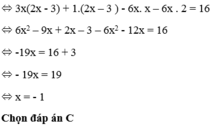
\(2x^2+6x-16=0\)
\(\Rightarrow2.\left(x^2+3x-8\right)=0\)
\(\Rightarrow x^2+3x-8=0\)
\(\Rightarrow x^2+2.x.\frac{3}{2}+\left(\frac{3}{2}\right)^2-8-\left(\frac{3}{2}\right)^2=0\)
\(\Rightarrow\left(x+\frac{3}{2}\right)^2-\frac{23}{4}=0\)
\(\Rightarrow\left(x+\frac{3}{2}\right)^2-\sqrt{\left(\frac{23}{4}\right)^2}=0\)
\(\Rightarrow\left(x+\frac{3}{2}+\frac{23}{4}\right).\left(x+\frac{3}{2}-\frac{23}{4}\right)=0\)
\(\Rightarrow\hept{\begin{cases}x+\frac{3}{2}+\frac{23}{4}=0\\x+\frac{3}{2}-\frac{23}{4}=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-\frac{29}{4}\\x=\frac{17}{4}\end{cases}}\)
leminhduc bạn pahir thay dấu { bằng [.