Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

What? Lớp 10? Mí bài nỳ dễ mak! Trên lp cs hc mak k giải đc thì thui lun!![]()

ĐKXĐ: \(x\ge2\)
\(\Leftrightarrow\sqrt{x-2-2\sqrt{x-2}+1}+\sqrt{x-2-6\sqrt{x-2}+9}=-x^2+4x-2\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-2}-1\right)^2}+\sqrt{\left(\sqrt{x-2}-3\right)^2}=-x^2+4x-2\)
\(\Leftrightarrow\left|\sqrt{x-2}-1\right|+\left|\sqrt{x-2}-3\right|=-x^2+4x-2\)
\(\Leftrightarrow\left|\sqrt{x-2}-1\right|+\left|3-\sqrt{x-2}\right|=2-\left(x-2\right)^2\)
Ta có: \(VP=2-\left(x-2\right)^2\le2\)
\(VT=\left|\sqrt{x-2}-1\right|+\left|3-\sqrt{x-2}\right|\ge\left|\sqrt{x-2}-1+3-\sqrt{x-2}\right|=2\)
\(\Rightarrow VT\ge VP\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\sqrt{x-2}-1\ge0\\3-\sqrt{x-2}\ge0\\x-2=0\end{matrix}\right.\) \(\Rightarrow\) Không tồn tại x thỏa mãn
Vậy pt vô nghiệm

a) đk \(\left\{{}\begin{matrix}2x+1\ge0\\x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\x\ne0\end{matrix}\right.\)
b) đk \(x+3>0\Leftrightarrow x>-3\)
c) \(\left\{{}\begin{matrix}x-1>0\\x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>1\\x\ge0\end{matrix}\right.\Leftrightarrow x>1\)
d) đk \(\left\{{}\begin{matrix}x^2-4\ne0\\x+1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x\ne\pm2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x\ne2\end{matrix}\right.\)

\(\left(x+5\right)\sqrt{2x^2+1}=x^2+x-5\left(đk:x\ge0\right)\)
\(< =>x\sqrt{2x^2+1}-0+5\sqrt{2x^2+1}-5=x\left(x+1\right)\)
\(< =>\frac{x^2\left(2x^2+1\right)}{x\sqrt{2x^2+1}}+\frac{25\left(2x^2+1\right)-25}{5\sqrt{2x^2+1}+5}=x\left(x+1\right)\)
\(< =>\frac{x\left(2x^2+1\right)}{\sqrt{2x^2+1}}+\frac{25.2x^2}{5\left(\sqrt{2x^2+1}+1\right)}-x\left(x+1\right)=0\)
\(< =>x\left[\frac{2x^2+1}{\sqrt{2x^2+1}}+\frac{10x}{\sqrt{2x^2+1}+1}-x-1\right]=0< =>x=0\)
đánh giá cái ngoặc to to bằng đk là được , hoặc có nghiệm nữa thì giải luôn

1.
a) 13\(\frac{1}{3}\) : 1\(\frac{1}{3}\) = 26 : (2x - 1)
<=> \(\frac{40}{3}:\frac{4}{3}\) = 13x - 26
<=> 10 + 26 = 13x
<=> 13x = 36
<=> x = \(\frac{36}{13}\)
b) 0,2 : 1\(\frac{1}{5}\) = \(\frac{2}{3}\) : (6x + 7)
<=> \(\frac{1}{5}:\frac{6}{5}\) = \(\frac{1}{9}x\) : \(\frac{2}{21}\)
<=> \(\frac{1}{6}\) = \(\frac{1}{9}x\) : \(\frac{2}{21}\)
<=> \(\frac{1}{9}x\) = \(\frac{2}{21}.\frac{1}{6}\) = \(\frac{1}{63}\)
<=> x = \(\frac{1}{7}\)
c) \(\frac{37-x}{x+13}\) = \(\frac{3}{7}\)
<=> (37 - x) . 7 = 3.(x + 13)
<=> 119 - 7x = 3x + 39
<=> -7x - 3x = 39 - 119
<=> -10x = -80
<=> x = 8
d) \(\frac{x-1}{x+5}=\frac{6}{7}\)
<=> 7(x - 1) = 6(x + 5)
<=> 7x - 7 = 6x + 30
<=> 7x - 6x = 30 + 7
<=> x = 37
e)
2\(\frac{2}{\frac{3}{0,002}}\) = \(\frac{1\frac{1}{9}}{x}\)
<=> \(\frac{1501}{750}\) = \(\frac{10}{9}:x\)
<=> x = \(\frac{10}{9}:\frac{1501}{750}\) = \(\frac{2500}{4503}\)
Bài 2. đề sai
Bài 3.
a) 6,88 : x = \(\frac{12}{27}\)
<=> x = 6,88 : \(\frac{12}{27}\)
<=> x = 15,48
b) 8\(\frac{1}{3}\) : \(11\frac{2}{3}\) = 13 : 2x
<=> \(\frac{25}{3}:\frac{35}{3}\) = 13 : 2x
<=> \(\frac{5}{7}=13:2x\)
<=> 2x = \(13:\frac{5}{7}\) = \(\frac{91}{5}\)
<=> x = 9,1

\(1+\sqrt{x^2-4x+3}-x=0\)
\(ĐK:\left\{{}\begin{matrix}\sqrt{x^2-4x+3\ge0}\\x-1\ge0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x\ge3\end{matrix}\right.\)
\(PT\Leftrightarrow\sqrt{x^2-4x+3}-\left(x-1\right)=0\)
\(\Leftrightarrow\frac{x^2-4x+3-\left(x-1\right)^2}{\sqrt{x^2-4x+3}+\left(x-1\right)}=0\)
\(\Leftrightarrow2-2x=0\Rightarrow x=1\left(tm\right)\)
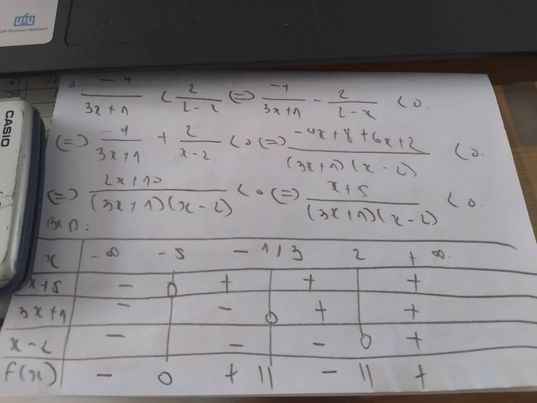

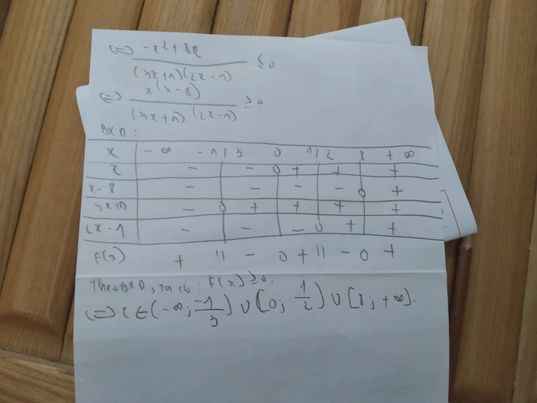
Đề có sai ko bạn ?
\(\left|\dfrac{1}{2}x\right|=3-2x\)(1)
Vì \(VT\ge0\Rightarrow3-2x\ge0\Leftrightarrow x\le\dfrac{3}{2}\)
\(\left(1\right)\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x=3-2x\\\dfrac{1}{2}x=-3+2x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\left(Chon\right)\\x=2\left(Loai\right)\end{matrix}\right.\)
Vậy....