Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) |x -1,7| = 2,3 => x - 1,7 = 2,3 hoặc x - 1,7 = -2,3
Với x - 1,7 = 2,3 => x = 4
Với x - 1,7 = -2,3 => x= -0,6
Vậy x = 4 hoặc x = -0,6
b) 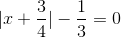 =>
=> 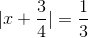
Suy ra: 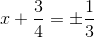
Với 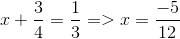
Với 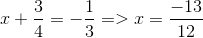

mình làm lại câu b) nha
b) |x-3|=-4
th1: x-3=-4
x=3+(-4)
x=-1
th2: x-3=4
x=3+4
x=7
b) \(\left|x-3\right|=-4\)
t/h1:\(x-3=-4\)
\(x=3-\left(-4\right)\)
\(x=7\)
t/h2:\(x-3=4\)
\(x=3-4\)
\(x=-1\)

a: =>|x-1/4|=3/4
=>x-1/4=3/4 hoặc x-1/4=-3/4
=>x=1 hoặc x=-1/2
b: \(\left|x+\dfrac{1}{2}\right|=\dfrac{1}{2}-\dfrac{9}{4}=\dfrac{2-9}{4}=-\dfrac{7}{4}\)(vô lý)
c: \(\Leftrightarrow\left[{}\begin{matrix}2x+5=1-x\\2x+5=x-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=-4\\x=-6\end{matrix}\right.\Leftrightarrow x\in\left\{-\dfrac{4}{3};-6\right\}\)
e: =>|3/2-x|=0
=>3/2-x=0
hay x=3/2

a) \(\left|x-1,7\right|=2,3\)
\(\Rightarrow\orbr{\begin{cases}x-1,7=2,3\\x-1,7=-2,3\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=4\\x=-0,6\end{cases}}\)
b) \(\left|x+\frac{3}{4}\right|-\frac{1}{3}=0\)
\(\Rightarrow\left|x+\frac{3}{4}\right|=\frac{1}{3}\)
\(\Rightarrow\orbr{\begin{cases}x+\frac{3}{4}=\frac{1}{3}\\x+\frac{3}{4}=-\frac{1}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=-\frac{5}{12}\\x=-\frac{13}{12}\end{cases}}\)

Ix-1,7I = 2,3
TH1: x - 1,7 = 2,3
=> x = 2,3 + 1,7
=> x = 4
TH2 : x - 1,7 = -2,3
=> x = -2,3 + 1,7
=> x = -0,6
b) Ix + 3/4I - 1/3 = 0
=> Ix + 3/4I = 0 + 1/3
=> x + 3/4 = 1/3
=> x = 1/3 - 3/4
=> x = -5/12
a.
\(\left|x-1,7\right|=2,3\)
\(x-1,7=\pm2,3\)
TH1:
\(x-1,7=2,3\)
\(x=2,3+1,7\)
\(x=4\)
TH2:
\(x-1,7=-2,3\)
\(x=-2,3+1,7\)
\(x=-0,6\)
Vậy x = 4 hoặc x = -0,6
b.
\(\left|x+\frac{3}{4}\right|-\frac{1}{3}=0\)
\(\left|x+\frac{3}{4}\right|=\frac{1}{3}\)
\(x+\frac{3}{4}=\pm\frac{1}{3}\)
TH1:
\(x+\frac{3}{4}=\frac{1}{3}\)
\(x=\frac{1}{3}-\frac{3}{4}\)
\(x=\frac{4-9}{12}\)
\(x=-\frac{5}{12}\)
TH2:
\(x+\frac{3}{4}=-\frac{1}{3}\)
\(x=-\frac{1}{3}-\frac{3}{4}\)
\(x=\frac{-4-9}{12}\)
\(x=-\frac{13}{12}\)
Vậy x = -5/12 hoặc x = -13/12.

Bài 1:
a) \(x^2-3=1\)
\(\Rightarrow x^2=1+3=4\)
\(\Rightarrow x=\pm2\)
b)\(2x^3+12=-4\)
\(\Rightarrow2x^3=-4-12=-16\)
\(\Rightarrow x^3=-8\)
\(\Rightarrow x=-2\)
c)\(\left(2x-3\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=4\\2x-3=-4\end{matrix}\right.\Leftrightarrow}\left[{}\begin{matrix}x=\dfrac{7}{2}\\-\dfrac{1}{2}\end{matrix}\right.\)
a) \(x^2-3=1\Rightarrow x^2=4\Rightarrow x=\pm2\)
b) \(2x^3+12=-4\Rightarrow2x^3=-16\)
\(\Rightarrow x^3=-\dfrac{16}{2}=-8=-2^3\)
\(\Rightarrow x=-2\)
c) \(\left(2x-3\right)^2=16\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=4\\2x-3=-4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
d,h,i,k cững tương tự....

a)
\(\left(3x+\dfrac{1}{3}\right)\left(x-\dfrac{1}{2}\right)=0\\ \Rightarrow\left[{}\begin{matrix}3x+\dfrac{1}{3}=0\\x-\dfrac{1}{2}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{9}\\x=\dfrac{1}{2}\end{matrix}\right.\)
b)
\(\left(x-\dfrac{3}{2}\right)\left(2x+1\right)>0\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-\dfrac{3}{2}>0\\2x+1>0\end{matrix}\right.\\\left\{{}\begin{matrix}x-\dfrac{3}{2}< 0\\2x+1< 0\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>\dfrac{3}{2}\\x>-\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x< \dfrac{3}{2}\\x< -\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x>\dfrac{3}{2}\\x< -\dfrac{1}{2}\end{matrix}\right.\)

bài 1)
a) \(\dfrac{11}{13}-\left(\dfrac{5}{42}-x\right)=-\left(\dfrac{15}{28}-\dfrac{11}{15}\right)
\)
\(\left(\dfrac{5}{42}-x\right)=\dfrac{11}{13}+\dfrac{15}{28}-\dfrac{11}{15}\)
\(x=\dfrac{5}{42}-\dfrac{3541}{5460}=-\dfrac{413}{780}\)
b) \(\left|x+\dfrac{4}{15}\right|-\left|-3,75\right|=-\left|2,15\right|\)
\(\left|x+\dfrac{4}{15}\right|=-\left|2,15\right|+\left|3,75\right|=1,6\)
\(\Rightarrow x+\dfrac{4}{15}=1,6\) hoặc \(x+\dfrac{4}{15}=-1,6\)
\(\Rightarrow x=\dfrac{4}{3}\) hoặc \(x=-\dfrac{28}{15}\)
c) \(\dfrac{5}{3}-\left|x-\dfrac{3}{2}\right|=-\dfrac{1}{2}\)
\(\Rightarrow\left|x-\dfrac{3}{2}\right|=\dfrac{5}{3}+\dfrac{1}{2}=\dfrac{13}{6}\)
\(\Rightarrow x-\dfrac{3}{2}=\dfrac{13}{6}\) hoặc \(x-\dfrac{3}{2}=-\dfrac{13}{6}\)
\(\Rightarrow x=\dfrac{11}{3}\) hoặc \(x=-\dfrac{2}{3}\)
d)\(\left(x-\dfrac{2}{3}\right).\left(2x-\dfrac{3}{2}\right)=0\)
\(\Rightarrow x-\dfrac{2}{3}=0\) hoặc \(2x-\dfrac{3}{2}=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=\dfrac{3}{4}\end{matrix}\right.\)
3) a) \(\left(x^{^2}-4\right)^{^2}+\left(x+2\right)^{^2}=0\)
Vì \(\left(x^{^2}-4\right)^{^2}\ge0,\left(x+2\right)^{^2}\ge0\) nên :
\(\left\{{}\begin{matrix}x^{^2}-4=0\\x+2=0\end{matrix}\right.\Rightarrow x=\pm2\)
b) \(\left(x-y\right)^{^2}+\left|y+2\right|=0\)
Vì \(\left\{{}\begin{matrix}\left(x-y\right)^{^2}\ge0\\\left|y+2\right|\ge0\end{matrix}\right.\) nên \(\left\{{}\begin{matrix}x-y=0\\y+2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x-y=0\\y=-2\end{matrix}\right.\Rightarrow x=-2;y=-2\)
c) \(\left|x-y\right|+\left|y+\dfrac{9}{25}\right|=0\)
Vì \(\left\{{}\begin{matrix}\left|x-y\right|\ge0\\\left|y+\dfrac{9}{25}\right|\ge0\end{matrix}\right.\) nên \(\left\{{}\begin{matrix}x-y=0\\y+\dfrac{9}{25}=0\end{matrix}\right.\Rightarrow y=-\dfrac{9}{25};x=-\dfrac{9}{25}\)
d) \(\left|\dfrac{1}{2}-\dfrac{1}{3}+x\right|=\left(-\dfrac{1}{4}\right)-\left|y\right|\)
\(\Rightarrow\left|\dfrac{1}{2}-\dfrac{1}{3}+x\right|+\left|y\right|=-\dfrac{1}{4}\)
Vì \(\left\{{}\begin{matrix}\left|\dfrac{1}{2}-\dfrac{1}{3}+x\right|\ge0\\\left|y\right|\ge0\end{matrix}\right.\) mà \(\left|\dfrac{1}{2}-\dfrac{1}{3}+x\right|+\left|y\right|=-\dfrac{1}{4}\) nên không tồn tại x,y thỏa mãn đề bài .

a/dễ --> tự lm
b/ \(\left(x-\dfrac{4}{7}\right)\left(1\dfrac{3}{5}+2x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{5}=0\\1\dfrac{3}{5}+2x=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\2x=\dfrac{8}{5}\Rightarrow x=\dfrac{4}{5}\end{matrix}\right.\)
Vậy...............
c/ \(\left(x-\dfrac{4}{7}\right):\left(x+\dfrac{1}{2}\right)>0\)
TH1: \(\left\{{}\begin{matrix}x-\dfrac{4}{7}>0\\x+\dfrac{1}{2}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>\dfrac{4}{7}\\x>-\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow x>\dfrac{4}{7}\)
TH2: \(\left\{{}\begin{matrix}x-\dfrac{4}{7}< 0\\x+\dfrac{1}{2}< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x< \dfrac{4}{7}\\x< -\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow x< -\dfrac{1}{2}\)
Vậy \(x>\dfrac{4}{7}\) hoặc \(x< -\dfrac{1}{2}\) thì thỏa mãn đề
d/ \(\left(2x-3\right):\left(x+1\dfrac{3}{4}\right)< 0\)
TH1: \(\left\{{}\begin{matrix}2x-3>0\\x+1\dfrac{3}{4}< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>1,5\\x< -\dfrac{7}{4}\end{matrix}\right.\)(vô lý)
TH2: \(\left\{{}\begin{matrix}2x-3< 0\\x+1\dfrac{3}{4}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x< 1,5\\x>-\dfrac{7}{4}\end{matrix}\right.\)\(\Rightarrow-\dfrac{7}{4}< x< 1,5\)
Vậy...................
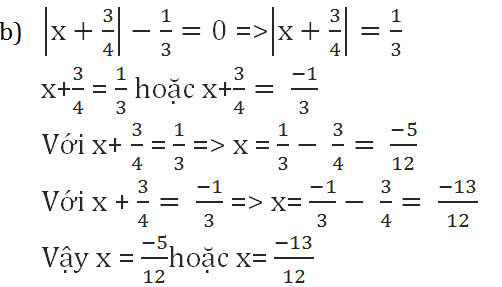
a) |x -1,7| = 2,3 => x - 1,7 = 2,3 hoặc x - 1,7 = -2,3
Với x - 1,7 = 2,3 => x = 4
Với x - 1,7 = -2,3 => x= -0,6
Vậy x = 4 hoặc x = -0,6
b)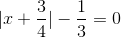 =>
=> 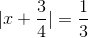
Suy ra: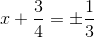
Với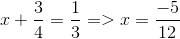
Với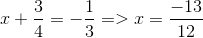
=>x-1,7=2,3 hoặc x-1,7=-2,3
=>x=2,3+1,7 hoặc x=-2,3+1,7
=>x=4 hoặc x= -0,6
vậy x=4 hoặc x=-0,6
b,\(|x+\dfrac{3}{4}|-\dfrac{1}{3}=0\)
\(|x+\dfrac{3}{4}|=\dfrac{1}{3}\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{3}\\x+\dfrac{3}{4}=-\dfrac{1}{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}-\dfrac{3}{4}\\x=-\dfrac{1}{3}-\dfrac{3}{4}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{12}\\x=-\dfrac{13}{12}\end{matrix}\right.\)
vậy x=-5/12 hoặc x= -13/12