Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi số cây trồng được của lớp 7A,7B,7C là a,b,c(cây)(a,b,c∈N*)
Áp dụng t/c dtsbn:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\Rightarrow\left\{{}\begin{matrix}a=12.4=48\\b=12.6=72\\c=12.3=36\end{matrix}\right.\)
Vậy....
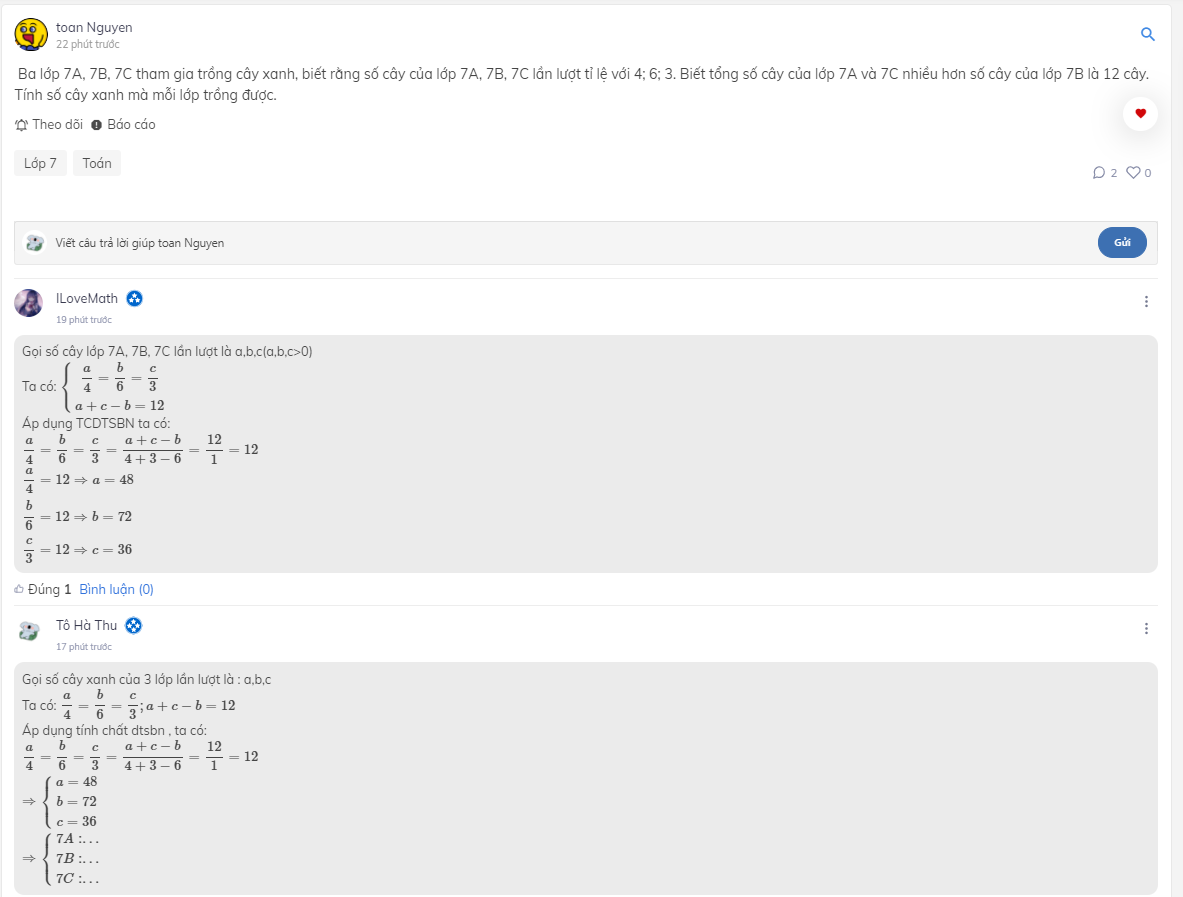
Gọi số cây lớp 7A, 7B, 7C lần lượt là a,b,c(a,b,c>0)
Ta có: \(\left\{{}\begin{matrix}\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}\\a+c-b=12\end{matrix}\right.\)
Áp dụng TCDTSBN ta có:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\dfrac{a}{4}=12\Rightarrow a=48\\ \dfrac{b}{6}=12\Rightarrow b=72\\ \dfrac{c}{3}=12\Rightarrow c=36\)
Gọi số cây xanh của 3 lớp lần lượt là : a,b,c
Ta có: \(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3};a+c-b=12\)
Áp dụng tính chất dtsbn , ta có:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\Rightarrow\left\{{}\begin{matrix}a=48\\b=72\\c=36\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}7A:...\\7B:...\\7C:...\end{matrix}\right.\)
Gọi số cây lớp 7A,7B,7C ll là a,b,c(cây;a,b,c>0)
Áp dụng t.c dtsbn:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a-b+c}{4-6+3}=\dfrac{12}{1}=12\\ \Leftrightarrow\left\{{}\begin{matrix}a=48\\b=72\\c=36\end{matrix}\right.\)
Vậy ..
\(\text{Gọi số cây lớp 7A; 7B; 7C trồng đc lần lượt là x; y; z}\)\(\text{Theo đề bài, ta có: }\)
\(\dfrac{x}{4}=\dfrac{y}{6}=\dfrac{z}{3}\)
\(\text{Áp dụng tính chất của hai dãy tỷ số bằng nhau, ta có:}\)
\(\dfrac{x}{4}=\dfrac{y}{6}=\dfrac{z}{3}=\dfrac{\left(x+z\right)-y}{\left(4+3\right)-6}=\dfrac{12}{1}=12\)
\(\left\{{}\begin{matrix}\dfrac{x}{4}=12;x=12.4=48\\\dfrac{y}{6}=12;y=12.6=72\\\dfrac{z}{3}=12;z=12.3=36\end{matrix}\right.\)
\(\text{Vậy số cây của 3 lớp 7A; 7B; 7C trồng đc lần lượt là 48; 72; 36}\)
\(\text{Nếu thấy hay thì cho xin cái li.ke nha bn ôi}\)
Gọi số cây lớp 7a, 7b, 7c trồng được lần lượt là a,b,c
Ta có\(\left\{{}\begin{matrix}\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}\\c-a=6\end{matrix}\right.\)
áp dụng t/c dtsbn ta có:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}=\dfrac{c-a}{5-2}=\dfrac{6}{3}=2\)
\(\dfrac{a}{2}=2\Rightarrow a=4\\ \dfrac{b}{3}=2\Rightarrow b=6\\ \dfrac{c}{5}=2\Rightarrow c=10\)
Gọi số cây 7A,7B,7C trồng lần lượt là a,b,c(cây;a,b,c∈N*)
Áp dụng tc dtsbn:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}=\dfrac{c-a}{5-2}=\dfrac{6}{3}=2\\ \Rightarrow\left\{{}\begin{matrix}a=4\\b=6\\c=10\end{matrix}\right.\)
Vậy ...
Gọi số cây mà `3` lớp trồng được lần lượt là `x,y,z (x,y,z \in \text {N*})`
Vì số cây của `3` lớp lần lượt tỉ lệ với `3:4:5`
Nghĩa là: `x/3=y/4=z/5`
Số cây trồng được của lớp `7A, 7B` nhiều hơn lớp `7C` là `40` cây
`-> x+y-z=40`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/3=y/4=z/5=(x+y-z)/(3+4-5)=40/2=20`
`-> x/3=y/4=z/5=20`
`-> x=20*3=60, y=20*4=80, z=20*5=100`
Vậy, số cây của `3` lớp lần lượt là `60` cây, `80` cây, `100` cây.
Gọi số cây trồng được của 3 lớp 7A,7B,7C lần lượt là \(x,y,z\)(cây) \((x,y,z \in N*)\)
Do số cây trồng được của 3 lớp 7A,7B,7C lần lượt tỉ lệ với 3,4,5 nên:\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Do số cây trồng được của 2 lớp 7A,7B nhiều hơn số cây trồng được của lớp 7C là 40 cây nên \(x+y-z=40\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y-z}{3+4-5}=\dfrac{40}{2}=20\)
Do đó:
\(\dfrac{x}{30}=20\Rightarrow x=60\)
\(\dfrac{y}{4}=20\Rightarrow y=80\) \(\left(TM\right)\)
\(\dfrac{z}{5}=20\Rightarrow z=100\)
Bài 1:
Gọi số học sinh lần lượt của lớp 7A và 7B lần lượt là a và b
Theo đề ta có
\(\frac{a}{b}=\frac{8}{9}\) \(\Rightarrow\) \(\frac{a}{8}=\frac{b}{9}\) và b - a = 5 (7A ít hơn 7B 5 học sinh)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
=> \(\frac{a}{8}=\frac{b}{9}=\frac{b-a}{9-8}=5\)
=> \(\frac{a}{8}=5\) \(\Rightarrow\) \(a=8\cdot5=40\)
=> \(\frac{b}{9}=5\) \(\Rightarrow\) \(b=9\cdot5=45\)
Vậy số học sinh lớp 7A là 40 học sinh
Số học sinh lớp 7A là 45 học sinh
Gọi số cây trồng của lớp 7A, 7B, 7C, 7D lần lượt là a, b, c,d
Theo đề ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{d}{6}\) và b - a = 5 (lớp 7A trồng ít hơn 7B 5 cây)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{d}{6}=\frac{b-a}{4-3}=5\)
=> \(\frac{a}{3}=5\) => a = 5 . 3 = 15
=> \(\frac{b}{4}=5\) => b = 4 . 5 = 20
=> \(\frac{c}{5}=5\) => c = 5 . 5 = 25
=> \(\frac{d}{6}=5\) => d = 6 . 5 = 30
Vậy số cây lớp 7A trồng được là: 15 cây
số cây lớp 7B trồng được là: 20 cây
số cây lớp 7C trồng được là: 25 cây
số cây lớp 7D trồng được là: 30 cây
Gọi số cây lớp 7A,7B,7C trồng được lần lượt là a(cây), b(cây),c(cây)
(Điều kiện: \(a\in Z^+;b\in Z^+;c\in Z^+\))
Số cây của lớp 7A,7B,7C lần lượt tỉ lệ với 6;4;5 nên ta có:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{5}\)
Tổng số cây trồng được của 2 lớp 7A,7B nhiều hơn của lớp 7C là 50 cây nên ta có: a+b-c=50
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b-c}{6+4-5}=\dfrac{50}{5}=10\)
=>a=60;b=40;c=50
Vậy: Lớp 7A trồng được 60 cây
Lớp 7B trồng được 40 cây
Lớp 7C trồng được 50 cây
Gọi x,y,z (cây) lần lượt là số cây trồng được của ba lớp 7A, 7B và 7C ( x, y, z \(\in\) N*)
Do số cây trồng được của ba lớp 7A,7B,7C lần lượt tỉ lệ với 6 ; 4 ; 5 nên:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{5}\)
Do tổng số cây của lớp 7B và 7C trồng được nhiều hơn của lớp 7A là 15 cây nên:
\(y+z-x=15\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{y+z-x}{4+5-6}=\dfrac{15}{3}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=5\cdot6=30\\y=5\cdot4=20\\z=5\cdot5=25\end{matrix}\right.\)
Vậy ...
#Đạt Đang Bận Thở
Gọi số cay trồng được của lớp 7A,7B,7C lần lượt là a,b,c
Theo đề, ta có: a/6=b/4=c/5
Áp dụng tính chất của DTSBN, ta được:
a/6=b/4=c/5=(a-c)/(6-5)=15
=>a=90; b=60; c=75
Bài 1:
a) \(\left|2x-3\right|=2\)
⇒ \(\left[{}\begin{matrix}2x-3=2\\2x-3=-2\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}2x=2+3=5\\2x=\left(-2\right)+3=1\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=5:2\\x=1:2\end{matrix}\right.\)
⇒ \(\left[{}\begin{matrix}x=\frac{5}{2}\\x=\frac{1}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{\frac{5}{2};\frac{1}{2}\right\}.\)
b) \(9.\left(x-1\right)^2-\frac{4}{9}:\frac{2}{9}=\frac{1}{4}\)
⇒ \(9.\left(x-1\right)^2-2=\frac{1}{4}\)
⇒ \(9.\left(x-1\right)^2=\frac{1}{4}+2\)
⇒ \(9.\left(x-1\right)^2=\frac{9}{4}\)
⇒ \(\left(x-1\right)^2=\frac{9}{4}:9\)
⇒ \(\left(x-1\right)^2=\frac{1}{4}\)
⇒ \(x-1=\pm\frac{1}{2}\)
⇒ \(\left[{}\begin{matrix}x-1=\frac{1}{2}\\x-1=-\frac{1}{2}\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=\frac{1}{2}+1\\x=\left(-\frac{1}{2}\right)+1\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=\frac{3}{2}\\x=\frac{1}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{\frac{3}{2};\frac{1}{2}\right\}.\)
Chúc bạn học tốt!
Vũ Minh Tuấn
ơi giải giúp mk câu 2 đi