VN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 10 2021
p(x)=\(x^3+ã^2+bx+c\)
với x=1 thì p(1)=0 hay
\(1+a+b+c=0\)
p(x) \(chia\)p(x-2) dư 6
với x=2 =>\(4a+2b+c+8=6< =>4a+2b+c=-2\)
tương tự với cái còn lại
xong bạn giải hệ phương trình bậc nhất ba ẩn là xong
HP
0
TV
2
MN
4 tháng 2 2018
\(x\)chia hết cho \(5\)
\(\Rightarrow\)\(x=5k\) \(\left(k\in N\right)\)
\(x\)chia \(7\)dư \(2\)
\(\Rightarrow\)\(x=7k+2\) \(\left(k\in N\right)\)
\(x\)chia \(9\)dư \(4\)
\(\Rightarrow\)\(x=9k+4\) \(\left(k\in N\right)\)
4 tháng 2 2018
x chia hết cho 5 => x có tận cùng là 0 hoặc 5
x chia 7 dư 2 => x - 2 chia hết cho 7 => x - 2 có tận cùng là 2 hoặc 7 và thuộc Ư(7) = { 7; 42; 77; 112; ...}
Vậy x thuộc {5; 40; 75; 110; ...}
x chia cho 9 dư 4 => x - 4 chia hết cho 9
x - 4 thuộc {9; 44; 79; 114; ...}
mà x - 4 chia hết cho 9 nên x thuộc x {9}
Vậy để x thỏa mãn điều kiện thì x = 9
CM
5 tháng 10 2017
+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m . ( - 1 ) 3 + ( m – 2 ) ( - 1 ) 2 – ( 3 n – 5 ) . ( - 1 ) – 4 n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
CM
4 tháng 3 2017
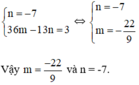
+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m.(-1)3 + (m – 2)(-1)2 – (3n – 5).(-1) – 4n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
