LL
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 7 2021
Vì BC và Cx là 2 tia đối nên \(\widehat{BCA}\) và \(\widehat{ACx}\) là 2 góc kề bù
\(\Rightarrow\widehat{ACB}+\widehat{ACx}=180^o\)
\(40^o+\widehat{ACx}=180^o\)
\(\widehat{ACx}=140^o\)
b) Ta có:\(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\) (tổng 3 góc trong 1 tam giác)
\(40^o+\widehat{ABC}+70^o=180^o\)
\(\widehat{ABC}=70^o\)(1)
Vì Oy là phân giác của \(\widehat{ACx}\) nên \(\widehat{xCy}=\dfrac{\widehat{ACx}}{2}=\dfrac{140^o}{2}=70^o\)(2)
Từ (1),(2) => \(\widehat{ABC}=\widehat{xCy}\)
c)Cặp góc đồng vị là \(\widehat{ABC}\) và \(\widehat{xCy}\)
19 tháng 10 2021
\(A=\dfrac{3}{2\cdot2}=\dfrac{3}{4}\\ A=\dfrac{3}{2\cdot5}=\dfrac{3}{10}\\ A=\dfrac{3}{2\cdot3}=\dfrac{1}{2}\)
NH
3
NA
1 tháng 12 2018
\(\left(\frac{2}{3}x-1\right)\left(\frac{3}{4}x+\frac{1}{2}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\frac{2}{3}x=1\\\frac{3}{4}x=-\frac{1}{2}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{2}\\x=-\frac{2}{3}\end{cases}}}\)
1 tháng 12 2018
Phương trình tích này:)
\(\Leftrightarrow\orbr{\begin{cases}\frac{2}{3}x-1=0\\\frac{3}{4}x+\frac{1}{2}=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{2}\\x=-\frac{2}{3}\end{cases}}\)
Em phải tự làm rồi đối chiếu kết quả xem có đúng ko :). Nếu ko thì kiểm tra sẽ ko làm đc bài :)
DT
13 tháng 12 2021
Câu này mình chưa học đến mình mới lớp 5 thôi đây toán lớp 7 chưa có ai chả lời được
YN
13 tháng 12 2021
Answer:
Câu 1:
\(5x+7y=40\)
\(\Rightarrow\hept{\begin{cases}5x=40\\7y=40\end{cases}}\Rightarrow\hept{\begin{cases}x=40:5\\y=40:7\end{cases}}\Rightarrow\hept{\begin{cases}x=8\\y=\frac{40}{7}\end{cases}}\)
Câu 2:
\(P=\frac{2x-5}{x+2}\left(x\ne-2\right)\)
\(=\frac{2x+4-9}{x+2}\)
\(=\frac{2x+4}{x+2}-\frac{9}{x+2}\)
\(=\frac{2\left(x+2\right)}{x+2}-\frac{9}{x+2}\)
\(=2-\frac{9}{x+2}\)
Mà để cho \(P\inℤ\) thì \(\frac{9}{x+2}\inℤ\)
\(\Rightarrow9⋮\left(x+2\right)\)
\(\Rightarrow x+2\inƯ\left(9\right)=\left\{\pm1;\pm3;\pm9\right\}\)
Có bảng sau:
| x+2 | -9 | -3 | -1 | 1 | 3 | 9 |
| x | -11 | -5 | -3 | 1 | 1 | 7 |
Vậy \(x\in\left\{-11;-5;-3;-1;1;7\right\}\) thì \(P\inℤ\)
24 tháng 9 2021
\(\dfrac{x}{6}=\dfrac{7}{4}\Rightarrow x=\dfrac{6\cdot7}{4}=\dfrac{21}{2}\\ \dfrac{3}{x}=\dfrac{21}{17}\Rightarrow x=\dfrac{3\cdot17}{21}=\dfrac{17}{7}\)
2 tháng 11 2017
câu 1:
2x=3y =>\(\dfrac{x}{3}=\dfrac{y}{2}\) (1)
5y=7z =>\(\dfrac{y}{7}=\dfrac{z}{5}\) (2)
Từ (1) và (2) suy ra
\(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\)=\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)
Dựa vào tính chất dãy tỉ số bằng nhau
Suy ra \(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)=\(\dfrac{3x+5z-7y}{63+50-98}=\dfrac{30}{15}=2\)
\(\dfrac{x}{21}=2\) =>x=2.21=42
\(\dfrac{y}{14}=2\) =>y=2.14=28
\(\dfrac{z}{10}=2\) =>z=2.10=20
Vậy x=42;y=28 và z=20
2 tháng 11 2017
Câu 2:
\(\dfrac{x^2}{5}=\dfrac{y^2}{4}\)
Dựa vào tính chất dãy tỉ số bằng nhau
Suy ra \(\dfrac{x^2-y^2}{5-4}\) =\(\dfrac{1}{1}=1\)
\(\dfrac{x^2}{5}=1\) =>x2=1.5=5 =>x=\(\sqrt{5}\) hay -\(\sqrt{5}\)
\(\dfrac{y^2}{4}=1\) => y2=1 => y=1 hay -1
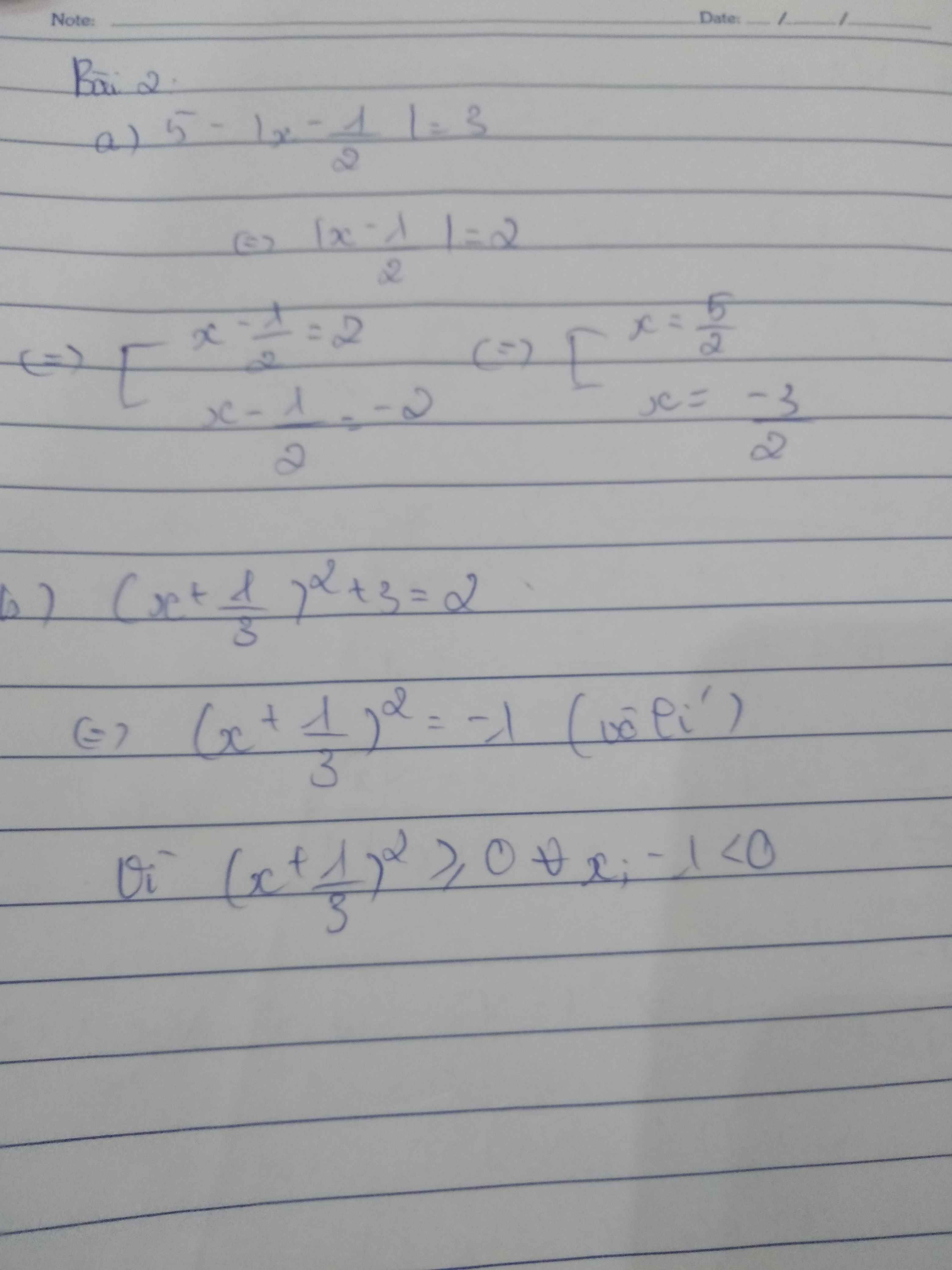
có gì ko hiểu bạn hỏi nhé
\(|2x+1|-|x-1|=3x\left(1\right)\)
Ta có:
\(2x+1=0\Leftrightarrow x=\frac{-1}{2}\)
\(x-1=0\Leftrightarrow x=1\)
Lập bảng xét dấu :
+) Với \(x< \frac{-1}{2}\Rightarrow\hept{\begin{cases}2x+1< 0\\x-1< 0\end{cases}\Rightarrow}\hept{\begin{cases}|2x+1|=-2x-1\\|x-1|=1-x\end{cases}\left(2\right)}\)
Thay (2) vào (1) ta được :
\(\left(-2x-1\right)-\left(1-x\right)=3x\)
\(-2x-1-1+x=3x\)
\(-2x+x-3x=1+1\)
\(-4x=2\)
\(x=\frac{-1}{2}\)( loại )
+) Với \(\frac{-1}{2}\le x< 1\Rightarrow\hept{\begin{cases}2x+1>0\\x-1< 0\end{cases}\Rightarrow\hept{\begin{cases}|2x+1|=2x+1\\|x-1|=1-x\end{cases}\left(3\right)}}\)
Thay (3) vào (1) ta được :
\(\left(2x+1\right)-\left(1-x\right)=3x\)
\(2x+1-1+x=3x\)
\(3x=3x\)( luôn đúng chọn )
+) Với \(x\ge1\Rightarrow\hept{\begin{cases}2x+1>0\\x-1>0\end{cases}\Rightarrow\hept{\begin{cases}|2x+1|=2x+1\\|x-1|=x-1\end{cases}\left(4\right)}}\)
Thay (4) vào (1) ta được :
\(\left(2x+1\right)-\left(x-1\right)=3x\)
\(2x+1-x+1=3x\)
\(2x-x-3x=-1-1\)
\(-2x=-2\)
\(x=1\)( chọn )
Vậy \(\frac{-1}{2}\le x\le1\)
\(\left|2x+1\right|-\left|x-1\right|=3x\Rightarrow\left|2x+1-1+x\right|\ge3x\)
\(\Leftrightarrow\left|3x\right|\ge3x\Rightarrow x\in\left\{x\inℤ|x\le0\right\}\)