Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1 : Tìm tất cả các phân số bằng phân số \(\frac{-32}{48}\) và có mẫu là số tự nhiên nhỏ hơn 15

2/ cái gì thế này ? không chứng minh được phải là <
1/ 12,5/40;.... nói chun có rất nhiều số

a) Giả sử phân số \(\frac{6n-7}{n-1}\) chưa tối tối giản
=> 6n -7 và n - 1 có ước chung là số nguyên tố
Gọi d = ƯC(6n - 7; n - 1)
\(\Leftrightarrow\hept{\begin{cases}6n-7⋮d\\n-1⋮d\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}6n-7⋮d\\6n-6⋮d\end{cases}}\)
\(\Leftrightarrow1⋮d\)
Vì \(d\in N;1⋮d\Leftrightarrow d=1\)
\(\LeftrightarrowƯCLN\left(6n-7;n-1\right)=1\)

Trước tiên ta rút gọn phân số 15/39 = 5/13

Ta phải nhân cả tử và mẫu của phân số với cùng một số tự nhiên sao cho tử và mẫu của nó là các số tự nhiên có hai chữ số.

Như vậy có sáu số là 2,3,4,5,6,7 thỏa mãn yêu cầu của đề bài.

\(\frac{20}{48}=\frac{5}{12}\)
\(\frac{5}{12}=\frac{10}{24}=\frac{15}{36}=\frac{20}{48}=\frac{25}{60}=\frac{30}{72}=\frac{35}{84}=\frac{40}{96}\)
\(\Rightarrow\frac{20}{48}=\frac{10}{24}=\frac{15}{36}=\frac{25}{60}=\frac{30}{72}=\frac{35}{84}=\frac{40}{96}\)

- Ta lấy phân số tối giản của phân số đã cho:
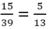
- Sau đó nhân tử và mẫu của phân số tối giản đó lần lượt với các số tự nhiên 2, 3, 4, 5, ... cho đến khi tử số và mẫu số vẫn là hai chữ số. Ta tìm được 6 phân số:
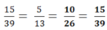
![]()
Ta có \(\frac{15}{39}\)= \(\frac{5}{13}\)
Ta có: \(\frac{5\cdot m}{13\cdot m}\)= \(\frac{5}{13}\)
Để tử và mẫu là sô có 2 chữ số thì => m thuộc { 2;3;4;5;6;7 }
Ta có: { \(\frac{10}{26}\); \(\frac{15}{39}\); \(\frac{20}{52}\); \(\frac{25}{65}\); \(\frac{30}{78}\); \(\frac{35}{91}\) }
Các phân số đó là: \(\frac{30}{78};\frac{20}{52};\frac{25}{65};\frac{10}{26};\frac{35}{91}\)