Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)3x+yi=(2y+1)(2−x)i⇔{3x=2y+1y=2−x⇔{x=1y=13x+yi=(2y+1)(2−x)i⇔{3x=2y+1y=2−x⇔{x=1y=1
b)2x+y−1=(x+2y−5)i⇔{2x+y−1=0x+2y−5=0⇔{x=−1y=3

1.
\(\lim\limits_{x\rightarrow\infty}\frac{3x-2}{x+1}=3\Rightarrow y=3\) là tiệm cận ngang
2.
\(\lim\limits_{x\rightarrow2}\frac{-2x}{x-2}=\infty\Rightarrow x=2\) là tiệm cận đứng
3.
\(\lim\limits_{x\rightarrow\infty}\frac{x-2}{x^2-1}=0\Rightarrow y=0\) là tiệm cận ngang
4.
\(\lim\limits_{x\rightarrow\infty}\frac{x-1}{x^2-x}=0\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow0}\frac{x-1}{x^2-x}=\infty\Rightarrow x=0\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow1}\frac{x-1}{x^2-x}=1\) hữu hạn nên \(x=1\) ko phải tiệm cận đứng
ĐTHS có 2 tiệm cận

Xét
\(y'=4x^3-4\left(m-1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x^2=m-1\end{cases}}\)
TH1:
\(m-1\le0\) thì hàm số đồng biến trên R
TH2: \(m-1>0\Rightarrow\orbr{\begin{cases}x=\sqrt{m-1}\\x=-\sqrt{m-1}\end{cases}}\)
Khi đó khoảng đồng biến của hàm số là \(\left(-\infty,-\sqrt{m-1}\right)\text{ và }\left(0,\sqrt{m-1}\right)\)
Muốn hàm số đồng biến trên (1,3) thì \(\left(1,3\right)\subset\left(0,\sqrt{m-1}\right)\Leftrightarrow3\le\sqrt{m-1}\Leftrightarrow m\ge10\)
Vậy \(\orbr{\begin{cases}m\le1\\m\ge10\end{cases}}\)
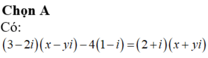
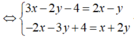
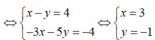



Đáp án C