Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 3. Dự đoán dấu "=" khi \(a=b=c=\frac{1}{\sqrt{3}}\)
Dùng phương pháp chọn điểm rơi thôi :)
LG
Áp dụng bđt Cô-si được \(a^2+b^2+c^2\ge3\sqrt[3]{a^2b^2c^2}\)
\(\Rightarrow1\ge3\sqrt[3]{a^2b^2c^2}\)
\(\Rightarrow\frac{1}{3}\ge\sqrt[3]{a^2b^2c^2}\)
\(\Rightarrow\frac{1}{27}\ge a^2b^2c^2\)
\(\Rightarrow\frac{1}{\sqrt{27}}\ge abc\)
Khi đó :\(B=a+b+c+\frac{1}{abc}\)
\(=a+b+c+\frac{1}{9abc}+\frac{8}{9abc}\)
\(\ge4\sqrt[4]{abc.\frac{1}{9abc}}+\frac{8}{9.\frac{1}{\sqrt{27}}}\)
\(=4\sqrt[4]{\frac{1}{9}}+\frac{8\sqrt{27}}{9}=\frac{4}{\sqrt[4]{9}}+\frac{8}{\sqrt{3}}=\frac{4}{\sqrt{3}}+\frac{8}{\sqrt{3}}=\frac{12}{\sqrt{3}}=4\sqrt{3}\)
Dấu "=" \(\Leftrightarrow a=b=c=\frac{1}{\sqrt{3}}\)
Vậy .........
2, \(A=\frac{a^2}{b+c}+\frac{b^2}{a+c}+\frac{c^2}{a+b}\)
\(A=\frac{a^2}{b+c}+\frac{b^2}{a+c}+\frac{c^2}{a+b}\)
\(A=\left[\frac{a^2}{b+c}+\frac{\left(b+c\right)}{4}\right]+\left[\frac{b^2}{a+c}+\frac{\left(a+c\right)}{4}\right]+\left[\frac{c^2}{a+b}+\frac{\left(a+b\right)}{4}\right]-\frac{\left(a+b+c\right)}{2}\)
Áp dụng BĐT AM-GM ta có:
\(A\ge2.\sqrt{\frac{a^2}{4}}+2.\sqrt{\frac{b^2}{4}}+2.\sqrt{\frac{c^2}{4}}-\frac{\left(a+b+c\right)}{2}\)
\(A\ge a+b+c-\frac{6}{2}\)
\(A\ge6-3\)
\(A\ge3\)
Dấu " = " xảy ra \(\Leftrightarrow\)\(\frac{a^2}{b+c}=\frac{b+c}{4}\Leftrightarrow4a^2=\left(b+c\right)^2\Leftrightarrow2a=b+c\)(1)
\(\frac{b^2}{a+c}=\frac{a+c}{4}\Leftrightarrow4b^2=\left(a+c\right)^2\Leftrightarrow2b=a+c\)(2)
\(\frac{c^2}{a+b}=\frac{a+b}{4}\Leftrightarrow4c^2=\left(a+b\right)^2\Leftrightarrow2c=a+b\)(3)
Lấy \(\left(1\right)-\left(3\right)\)ta có:
\(2a-2c=c+b-a-b=c-a\)
\(\Rightarrow2a-2c-c+a=0\)
\(\Leftrightarrow3.\left(a-c\right)=0\)
\(\Leftrightarrow a-c=0\Leftrightarrow a=c\)
Chứng minh tương tự ta có: \(\hept{\begin{cases}b=c\\a=b\end{cases}}\)
\(\Rightarrow a=b=c=2\)
Vậy \(A_{min}=3\Leftrightarrow a=b=c=2\)

Bài 1:
Áp dụng BĐT AM-GM ta có:
\(a-\dfrac{a^2}{a+b^2}=\dfrac{ab^2}{a+b^2}\le\dfrac{ab^2}{2b\sqrt{a}}=\dfrac{b\sqrt{a}}{2}\)
Tương tự cho các BĐT còn lại cũng có:
\(b-\dfrac{b^2}{b+c^2}\le\dfrac{c\sqrt{b}}{2};c-\dfrac{c^2}{c+a^2}\le\dfrac{a\sqrt{c}}{2}\)
Sau đó cộng theo vế các BĐT trên
\(\dfrac{a^2}{a+b^2}+\dfrac{b^2}{b+c^2}+\dfrac{c^2}{c+a^2}\ge3-\dfrac{1}{2}\left(b\sqrt{a}+c\sqrt{b}+a\sqrt{c}\right)\)
\(\ge3-\dfrac{1}{2}\sqrt{\left(a+b+c\right)\left(ab+bc+ca\right)}\)
\(\ge3-\dfrac{1}{2}\sqrt{\left(a+b+c\right)\cdot\dfrac{\left(a+b+c\right)^2}{3}}=3-\dfrac{3}{2}=\dfrac{3}{2}\)
Đẳng thức xảy ra khi \(a=b=c=1\)
Bài 2:
Áp dụng BĐT AM-GM ta có:
\(\dfrac{a}{\sqrt{2b^2+2c^2-a^2}}=\dfrac{\sqrt{3}a^2}{\sqrt{3a^2\left(2b^2+2c^2-a^2\right)}}\)
\(\ge\dfrac{\sqrt{3}a^2}{\dfrac{3a^2+2b^2+2c^2-a^2}{2}}=\dfrac{\sqrt{3}a^2}{a^2+b^2+c^2}\)
Tương tự cho các BĐT còn lại ta có:
\(\dfrac{b}{\sqrt{2a^2+2c^2-b^2}}\ge\dfrac{\sqrt{3}b^2}{a^2+b^2+c^2};\dfrac{c}{\sqrt{2a^2+2b^2-c^2}}\ge\dfrac{\sqrt{3}c^2}{a^2+b^2+c^2}\)
Cộng theo vế 3 BĐT trên ta có:
\(VT\ge\dfrac{\sqrt{3}\left(a^2+b^2+c^2\right)}{a^2+b^2+c^2}=\sqrt{3}=VP\)
Đẳng thức xảy ra khi \(a=b=c\)

Ta có:
\(\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2=9\\ \Leftrightarrow a+b+c+2\sqrt{ab}+2\sqrt{bc}+2\sqrt{ac}=9\\ \Leftrightarrow\sqrt{ab}+\sqrt{bc}+\sqrt{ac}=2\)
\(\Rightarrow\dfrac{\sqrt{a}}{a+2}+\dfrac{\sqrt{b}}{b+2}+\dfrac{\sqrt{c}}{c+2}=\dfrac{\sqrt{a}}{a+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}+\dfrac{\sqrt{b}}{b+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}+\dfrac{\sqrt{c}}{c+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}\\ =\dfrac{\sqrt{a}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)}+\dfrac{\sqrt{b}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)}+\dfrac{\sqrt{c}}{\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{a}+\sqrt{c}\right)}\\ =\dfrac{\sqrt{a}\left(\sqrt{b}+\sqrt{c}\right)+\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)+\sqrt{c}\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{a}+\sqrt{c}\right)}\\ =\dfrac{2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{a}+\sqrt{c}\right)}\\ =\dfrac{4}{\sqrt{\left(\sqrt{a}+\sqrt{b}\right)^2\left(\sqrt{b}+\sqrt{c}\right)^2\left(\sqrt{a}+\sqrt{c}\right)^2}}\)\(=\dfrac{4}{\sqrt{\left(a+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)\left(b+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)\left(c+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)}}\\ =\dfrac{4}{\sqrt{\left(a+2\right)\left(b+2\right)\left(c+2\right)}}\)

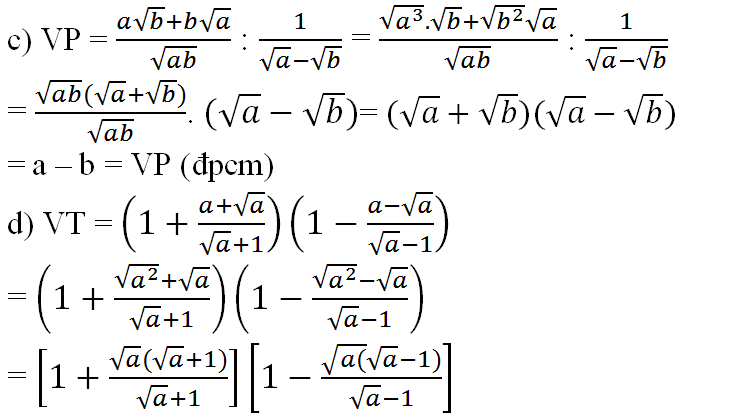
⚽⚽