Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho hàm số : \(y=f\left(x\right)=\dfrac{2}{3}x+5\) với \(x\in R\)
Giả sử : \(x_1< x_2\)
\(f\left(x_1\right)=\dfrac{2}{3}x_1+5\)
\(f\left(x_2\right)=\dfrac{2}{3}x_2+5\)
Từ \(x_1< x_2\) \(\Rightarrow\dfrac{2}{3}x_1< \dfrac{2}{3}x_2\)
\(\Rightarrow\dfrac{2}{3}x_1+5< \dfrac{2}{3}x_2+5\)
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
Vậy hàm số đồng biến trên \(R\)

Từ x1 < x2 và 3 > 0
suy ra : 3x1< 3x2 hay f(x1) < f(x2 ).
Vậy hàm số đã cho đồng biến trên R.

Thế \(x=2,x=\frac{1}{2}\)thì được
\(\hept{\begin{cases}f\left(2\right)+3f\left(\frac{1}{2}\right)=4\\f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}f\left(2\right)=-\frac{13}{32}\\f\left(\frac{1}{2}\right)=\frac{47}{32}\end{cases}}\)

Bài 1:
Ta có: xy ≤ (x + y)²/4 = 1/4, dấu = xảy ra khi x = y = 1/2
P = (x² + 1/y²)(y² + 1/x²) = (xy)² + 1 + 1 + 1/(xy)²
= (xy)² + 1/[256(xy)²] + 255/[256(xy)²] + 2
ta có:
(xy)² + 1/[256(xy)²] ≥ 2 √(1/256) = 1/8. dấu = xảy ra khi x = y = 1/2
255/[256(xy)²] + 2 ≥ 255/(256.1/16) + 2 = 287/16. dấu = xảy ra khi x = y = 1/2
cộng theo vế → P ≥ 1/8 + 287/16 = 289/16
vậy GTNN của P là 289/16, đạt được khi x = y = 1/2


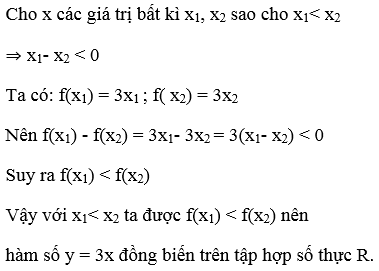
Sửa đề bài ( thêm ) . Tìm tất cả các hàm \(f:ℝ\rightarrowℝ\)