Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Đáp án D
Ta có y = 2 x - m - 1 x 2 + 1 x - 1 = 2 x - x m - 1 + 1 x 2 x - 1 = 2 = x x . m - 1 + 1 x 2 1 - 1 x
Đồ thị hàm số đã cho có hai đường TCN ⇔ m - 1 + 1 x 2 > 0 ; ∀ x ∈ ℝ ⇔ 1 - m < 0 ⇔ m > 1 .

Chọn B
Điều kiện để đồ thị có tiệm cận: m ≠ - 3
Tâm đối xứng I(1;-m) là giao điểm của hai đường tiệm cận.
Khi đó, I ∈ d ⇔ m = - 3 (loại). Vậy không tồn tại m thỏa mãn.

Đáp án A.
Ta có 2 x + 3 m x 2 + 1 = 2 x + 3 x 1 m + 1 x 2 ⇒ lim x → − ∞ 2 x + 3 x = lim x → − ∞ 2 x + 3 − x = − 2 và
lim x → + ∞ 2 x + 3 x = lim x → + ∞ 2 x + 3 x = 2 . Từ đó, suy ra các giới hạn lim x → − ∞ 2 x + 3 m x 2 + 1 ; lim x → + ∞ 2 x + 3 m x 2 + 1 tồn tại và hữu hạn khi và chỉ khi các giới hạn lim x → − ∞ m + 1 x 2 ; lim x → + ∞ m + 1 x 2 tồn tại, hữu hạn và khác không. Do lim x → ± ∞ 1 x 2 = 0 các giới hạn vừa nêu tồn tại, hữu hạn và khác 0 khi và chỉ khi m > 0.
Chú ý và Lỗi sai
* Định nghĩa: Cho hàm số y = f x xác định trên a ; + ∞ ; − ∞ ; b ; − ∞ ; + ∞
Nếu lim x → + ∞ f x = y 0 lim x → − ∞ f x = y 0 thì y = y 0 là tiệm cận ngang.
Từ định nghĩa tiệm cận ngang của đồ thị hàm số suy ra các giá trị m cần tìm là các giá trị sao cho tồn tại giới hạn của hàm số đã cho khi x tiến ra + ∞ và khi x tiến ra - ∞ , đồng thời hai giới hạn đó phải khác nhau.

Đáp án là D.
Đồ thị hàm số có bốn đường tiệm cận khi phương trình m 2 x 2 + m − 1 = 0 có hai nghiệm phân biệt khác -1 ⇔ m 2 ≠ 0 − m 2 m − 1 > 0 ⇔ m ≠ 0 m < 1 .

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

Ta có ![]() đồ thị hàm số luôn có TCN y = 1
đồ thị hàm số luôn có TCN y = 1
Do đó để ycbt thỏa mãn 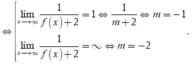
Chọn C.
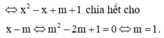
Để hàm số có 2 tiệm cận ngang thì phải tồn tại lim x → ∞ y ≠ lim x → - ∞ y
Ta có
lim x → ∞ y = lim x → ∞ 3 x + 2018 m x 2 + 5 x + 6 = lim x → ∞ y 3 + 2018 x m + 5 x + 6 x 2 = 3 m
tồn tại khi m > 0
lim x → - ∞ y = lim x → - ∞ 3 x + 2018 m x 2 + 5 x + 6 = lim x → - ∞ y 3 + 2018 x m + 5 x + 6 x 2 = - 3 m
tồn tại khi .
Khi đó hiển nhiên lim x → ∞ y ≠ lim x → - ∞ y . Vậy m > 0
Đáp án D