
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

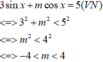

\(\Leftrightarrow1-cos^2x+2cosx-2+m=0\)
\(\Leftrightarrow cos^2x-2cosx+1=m\)
\(\Leftrightarrow\left(cosx-1\right)^2=m\)
Do \(-1\le cosx\le1\Rightarrow0\le\left(cosx-1\right)^2\le4\)
\(\Rightarrow0\le m\le4\)

Có tất cả bao nhiêu tham số m đề phương trình sau vô nghiệm với ẩn x, #Hỏi cộng đồng OLM #Toán lớp 11


3.
Hàm trùng phương \(f\left(x\right)=ax^4+bx^2+c\) với \(a\ne0\) đồng biến trên \(\left(0;+\infty\right)\) khi và chỉ khi:
\(\left\{{}\begin{matrix}a>0\\b\ge0\end{matrix}\right.\) \(\Leftrightarrow m\ge0\)
Hoặc giải bt: \(y'=4x^3+2mx\ge0\) ;\(\forall x>0\)
\(\Leftrightarrow2x\left(x^2+m\right)\ge0\)
\(\Leftrightarrow x^2+m\ge0\)
\(\Leftrightarrow x^2\ge-m\)
\(\Leftrightarrow-m\le min\left(x^2\right)=0\Rightarrow m\ge0\)
1.
Giả sử tiếp tuyến d có 1 vtpt là \(\left(a;b\right)\) với \(a^2+b^2>0\)
\(\Rightarrow cos30^0=\frac{\sqrt{3}}{2}=\frac{\left|a-2b\right|}{\sqrt{\left(a^2+b^2\right)\left(1^2+\left(-2\right)^2\right)}}=\frac{\left|a-2b\right|}{\sqrt{5\left(a^2+b^2\right)}}\)
\(\Leftrightarrow4\left(a-2b\right)^2=15\left(a^2+b^2\right)\)
\(\Leftrightarrow11a^2+16ab-b^2=0\)
Nghiệm xấu quá nhìn muốn nản, bạn tự làm tiếp :)
2.
\(y'=cosx-2sinx+2m-5\)
Hàm số đồng biến trên TXĐ khi và chỉ khi \(y'\ge0\) ; \(\forall x\)
\(\Leftrightarrow cosx-2sinx+2m-5\ge0\) ;\(\forall x\)
\(\Leftrightarrow2m-5\ge2sinx-cosx\)
\(\Leftrightarrow2m-5\ge f\left(x\right)_{max}\) với \(f\left(x\right)=2sinx-cosx\)
Ta có: \(f\left(x\right)=2sinx-cosx=\sqrt{5}\left(\frac{2}{\sqrt{5}}sinx-\frac{1}{\sqrt{5}}cosx\right)=\sqrt{5}sin\left(x-a\right)\)
Với \(a\in\left(0;\pi\right)\) sao cho \(cosa=\frac{2}{\sqrt{5}}\)
\(\Rightarrow f\left(x\right)\le\sqrt{5}\Rightarrow2m-5\ge\sqrt{5}\Rightarrow m\ge\frac{5+\sqrt{5}}{2}\)

ngại viết quá hihi, mà hơi ngáo tí cái dạng này lm rồi mà cứ quên
bài trước mk bình luận bạn đọc chưa nhỉ

Để pt đã cho vô nghiệm thì:
\(1^2+\left(m-1\right)^2< \left(\sqrt{5}\right)^2\)
\(\Leftrightarrow\left(m-1\right)^2< 4\)
\(\Rightarrow-2< m-1< 2\)
\(\Rightarrow-1< m< 3\)