
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Điều kiện x ≥ − 2
Đặt t = x + 2 t ≥ 0 ⇒ x = t 2 − 2
Khi đó phương trình tương đương
5 − t 2 + t + 2 − 5 m = 0 ⇔ m = 5 − t 2 + t + 1
Xét hàm số f t = 5 − t 2 + t + 1 ; t ≥ 0.
Ta có:
f ' t = − 2 t + 1 5 − t 2 + t + 1 ; f ' t = 0 ⇔ t = 1 2
Từ bảng biến thiên ra suy ra phương trình có nghiệm thì 0 < m ≤ 5 5 4

Đáp án D.
Đặt t = cos 3 x , ( - 1 ≤ t ≤ 1 ) Phương trình trở thành 2 t 2 + ( 3 - 2 m ) t + m - 2 = 0
Ta có ∆ = 2 m - 5 2 Suy ra phương trình có hai nghiệm t 1 = 1 2 t 2 = m - 2
Trường hợp 1:
Với t 1 = 1 2 → cos 3 x = 1 2 ⇔ 3 x = π 3 + k 2 π 3 x = - π 3 + k 2 π ⇔ x = π 9 + k 2 π 3 x = - π 9 + k 2 π 3
* Với x = π 9 + k 2 π 3 và x ∈ - π 6 ; π 3 thì - π 6 < - π 9 + k 2 π 3 < π 3 ⇔ 1 12 < k < 2 3
Do k ∈ ℤ nên k = 0 → x = - π 9
* Với x = - π 9 + k 2 π 3 và x ∈ - π 6 ; π 3 thì - π 6 < - π 9 + k 2 π 3 < π 3 ⇔ - 1 12 < k < 2 3
Do k ∈ ℤ nên k = 0 → x = - π 9
Suy ra phương trình đã cho luôn có hai nghiệm trên khoảng - π 6 ; π 3
Trường hợp 2: Với t 2 = m - 2 → cos 3 x = m - 2 Xét f ( x ) = cos 3 x trên - π 6 ; π 3
Đạo hàm f ' ( x ) = - 3 sin 3 x ; f ' ( x ) = 0 ⇔ x = 0 ∈ - π 6 ; π 3
Bảng biến thiên:
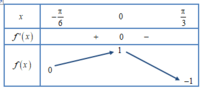
Để phương trình đã cho có 3 nghiệm trên
-
π
6
;
π
3
khi và chỉ khi phương trình
cos
3
x
=
m
-
2
có 1 nghiệm trên
-
π
6
;
π
3
, hay đồ thị
f
(
x
)
=
cos
3
x
cắt đường thẳng
y
=
m
-
2
tại đúng 1 điểm. Quan sát bảng biến thiên, suy ra
-
1
≤
m
-
2
<
0
⇔
1
≤
m
<
2

Đáp án C
6 x − 3 − m 2 x − m = 0 ⇔ m = 6 x + 3.2 x 2 x + 1
Xét hàm số f x = 6 x + 3.2 x 2 x + 1 trên khoảng 0 ; 1
f ' x = 6 x .2 x ln 6 − ln 2 + 6 x ln 6 + 3.2 x ln 2 2 x + 1 2 > 0 do đó hàm số y = f x đồng biến trên khoảng 0 ; 1 .
Phương trình f x = m có nghiệm trong khoảng 0 ; 1 ⇔ f 0 < m < f 1 ⇔ 2 < m < 4 .