
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


n nhỏ nhất có 12 ước
n= 22.3.5 = 60
=>201760 =20174.15 = (....1)15 = .....1
Vậy chữ só tận cùng là 1

Gọi số phải tìm là n; số chính phương đó là a; gọi b là số tự nhiên mà n là lập phương của nó.
Ta thấy n chia hết cho 2 và 3 (vì số chính phương hay lập phương của một số tự nhiên đều là số tự nhiên) nên để n nhỏ nhất, ta chọn n = 2x.3y (x và y khác 0).
n : 2 = 2x.3y : 2 = 2x-1.3y = a2 suy ra x - 1 và y đều chia hết cho 2 hay đều là số chẵn.
n : 3 = 2x.3y : 3 = 2x.3y-1 = b3 suy ra x và y - 1 đều chia hết cho 3.
Từ x - 1 chia hết cho 2 và x chia hết cho 3, để nhỏ nhất ta chọn x = 3
Từ y chia hết cho 2 và y - 1 chia hết cho 3, để nhỏ nhất ta chọn y = 4
Vậy n = 23.34 = 648
Số cần tìm là 648.

Ư(12)=(1,2,3,4,6,12)
Thay lần lượt ta có n+1=1 <=> n = 0
Bạn thay lần lượt nhé!

a) Vì nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}
Ta có bảng sau:
n + 1 | 1 | 2 | 3 | 6 |
n | 0 | 1 | 2 | 5 |
Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}
Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a và y = 2b.35
Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là và bội chung nhỏ nhất của hai số là 23.36.
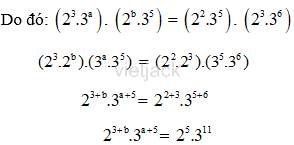
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2
a + 5 = 11. Suy ra a = 11 – 5 = 6
Vậy a = 6; b = 2.
Gọi x = 23.3a và y = 2b.35
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là 22.35 và bội chung nhỏ nhất của hai số là 23.36
Ta được x.y= 22.35.23.36=22.23.35.36=25.31122.35.23.36=22.23.35.36=25.311
Mà xy =23+b.3a+523+b.3a+5
Ta được 5=3+b và 11=a+5
Vậy b=2 và a=6

a: \(n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)

a: \(\Leftrightarrow n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)

mình có biết đâu, mình cũng đang hỏi bài này