Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi các chữ số của chúng lần lượt là; a,b,c
theo đề bài ta có:
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)
vì số đó là bội của 72 nên là bội của 9"
\(\Leftrightarrow a+b+c⋮9\)
áp dụng tính chất dãy tỉ sô bằng nhau ta có:
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\Rightarrow\frac{a}{6}=\frac{b}{6}=\frac{c}{6}\Rightarrow\frac{a+b+c}{6+6+6}\)
ta có:\(\frac{a}{1}\)là số nguyên nên: \(a+b+c⋮6\)
vậy tù đó => \(BC\left(9;6\right)=B\left(18\right)\)
TA CÓ;\(3\le a+b+c\le27\rightarrow a+b+c=18\)
\(\Leftrightarrow\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=3\)
Vậy:\(\frac{a}{1}=3\Rightarrow a=3\)
\(\frac{b}{2}=3\Rightarrow b=6\)
\(\frac{c}{3}=3\Rightarrow c=9\)
vậy số cần tím là:\(3.6.9=369\)
Shop hoa đỏ khách khảo khi he is rửa thực thực e which i ta được số is do Hà sĩ Hà to us đi Hà Huy đã đi ra đi Hà đi Hà gia giải khát social H

Gọi các chữ số của số đó là a,b,c (a<b<c)
Theo đề ta có \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)
Vì số đó là bội của 72 nên cũng là bội của 9 =>\(a+b+c⋮9\) (1)
Có\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\) =>\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{a+b+c}{6}\) Ta có \(\frac{a}{1}\) là số nguyên nên \(a+b+c⋮6\) (2)
Từ (1) và (2) => a+b+c \(\in BC\left(9;6\right)=B\left(18\right)\)
Ta có \(3\le a+b+c\le27\) nên a+b+c=18
=> \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{18}{6}=3\)
=>a=3, b=6, c=9
Vậy số cần tìm là 369

Gọi ba chữ số của số phải tìm là a, b, c
![]()
Số phải tìm là bội của 18 nên số đó chia hết cho 9 , do đó a + b + c= 9 hoặc a + b + c = 18 hoặc a + b + c =27
Theo đề bài, các chữ số của số đó tỉ lệ với 1;2;3 nên
a 1 = b 2 = c 3
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
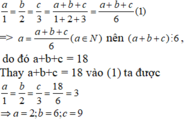
Lại có số phải tìm là bội của 18 nên chữ số hàng đơn vị của nó là số chẵn, do đó có hai số thỏa mãn đề bài là 396;936
Đáp án cần chọn là C

Gọi a, b,c lần lượt tỉ lệ với 1,2,3
a/1=b/2=c/3 và a+b+c=18
Áp dụng tính chất dãy tiwr số bằng :
a/1=b/2=c/3=a+b+c/1+2+3=18/6=3
Suy ra :a/1=3=>a=3
b/2=3=>b=6
c/3=3=>c=9

Gọi số cần tìm là x và các chữ số của x lần lượt là a;b;c Nếu x chia hết cho 18=>xchia hết cho 2 và 9 nên x chẵn Ta có a;b;c tỉ lệ với 1;2;3 thì nhân theo hệ quả ta được các số 123;246;369 Mà x chia hết cho 9 nên các số thõa mãn yêu cầu là 396 Vậy số cần tìm là 396

gọi 3 chữ số của số cần tìm là a,b,c ( a,b,c \(\in\)N ; a\(\ne\)0, a,b,c, \(\le\)9 )
Theo đầu bài ta có :
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)\(\Rightarrow\frac{a}{1}=\frac{a+b+c}{1+2+3}\)\(\Rightarrow a=\frac{a+b+c}{6}\)
Do vậy : a + b + c \(⋮\)6 ( 1 )
Mặt khác số đó chia hết cho 18 nên số đó chia hết cho 9 \(\Rightarrow\)a + b + c \(⋮\)9 ( 2 )
Mà 0 < a + b + c \(\le\)27 ( 3 )
Từ ( 1 ), ( 2 ) và ( 3 ) \(\Rightarrow\)a + b + c \(⋮\)18
Ta có : \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=3\)\(\Rightarrow a=3,b=6,c=9\)
\(\Rightarrow\)số đó là 396 hoặc 936

Gọi các chữ số trong số cần tìm lần lượt là a;b;c
Vơi \(a:b:c=1:2:3\)
\(\Rightarrow\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)
Vì số đó chia hết cho 72
=> số đó chia hết cho 8 và 9
Mà \(0< a+b+c< 27\)
=> \(\left[\begin{array}{nghiempt}a+b+c=9\\a+b+c=18\end{array}\right.\)
(+) Với a+b+c=9
Áp dụng tc của dãy tỉ số bằng nhau ta có
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{a+b+c}{1+2+3}=\frac{9}{6}=\frac{3}{2}\)
\(\Rightarrow\begin{cases}a=\frac{3}{2}\\b=3\\c=\frac{9}{2}\end{cases}\) ( Loại )
(+) Với a+b+c=18
Áp dụng tc của dãy tỉ số bằng nhau ta có
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{a+b+c}{1+2+3}=\frac{18}{6}=3\)
\(\Rightarrow\begin{cases}a=3\\b=6\\c=9\end{cases}\)
=> Số cần tìm \(\in\left\{369;396;936;963;639;693\right\}\)
Mặt khác số cần tìm chia hết cho 8
=> Số cần tìm là 936
Gọi abc là số cần tìm.
\(\Rightarrow abc⋮27\Rightarrow abc⋮9\Rightarrow a+b+c⋮9\)
Có: \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{a+b+c}{1+2+3}\)
Mà: \(0\le a+b+c\le27\Rightarrow a+b+c\in\left\{9;18;27\right\}\)
Xét các yêu cầu tỉ lệ 1,2,3 được \(\left(a,b,c\right)=\left(3,6,9\right)\)

Vì số đó là bội của 18 => số đó chia hết cho 2 và 9
=> tổng các cs của nó chia hết cho 9 và có tận cùng là số chẵn
mà các cs tỉ lệ với 1 : 2 : 3 ta cũng có các tỉ lệ 2 : 4 : 6 và 3 : 6 : 9
=> tỉ lệ 3 : 6 : 9 chia hết cho 9 ( chọn )
mà số đó chia hết cho 2
=> có 2 số thỏa mãn đề bài là 396 và 936

Số tự nhiên có 3 chữ số là bội của số 72 là : 144, 216, 288, 360, 432, 504, 576; 648; 720; 792; 864 vả 936. Trong các số tên chỉ có số 936 là thỏa mãn điều kiện các số từ nhỏ đến lớn theo tỷ lệ 1:2:3
nó chỉ sắp xếp theo thứ tự nhỏ đến lớn và tỉ lệ vs 1;2;3 ,ta có thể đảo vị trí các chữ số cho nhau mà