Tìm số tự nhiên a b c d e , biết rằng 2 a 15 b : c d e = 90

Tìm số tự nhiên a b c d e , biết rằng 2 a 15 b : c...

SK

Sakura Kinomoto

6 tháng 11 2014 - olm

cho a,b,c,d,e là số tự nhiên, chứng minh rằng: tích (a+b)(b+c)(c+d)(d+e)(e+a) chia hết cho 2

#Toán lớp 6

1

AH

Akai Haruma

Giáo viên

28 tháng 6

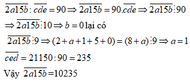
Lời giải:

Giả sử tích trên lẻ. Khi đó:

$a+b, b+c, c+d, d+e, e+a$ lẻ

$\Rightarrow (a+b)+(b+c)+(c+d)+(d+e)+(e+a)$ lẻ (tổng của 5 số lẻ là 1 số lẻ)

$\Rightarrow 2(a+b+c+d+e)$ lẻ (vô lý)

Do đó điều giả sử là sai. Tức là tích $(a+b)(b+c)(c+d)(d+e)(e+a)$ chẵn.

Đúng(0)

TN

Tuyết Nhi TV

28 tháng 10 2021

Tìm số tự nhiên x, biết : x E Ư(30) và 3 < x < 6 A. 4 B. 5 C. 6 D. 10 31. Tìm số tự nhiên x, biết : x E B(8) và 20 < x < 30 A. 23 B.24 C. 25 D. 26

#Toán lớp 6

3

I

ILoveMath

28 tháng 10 2021

B

Đúng(1)

NH

Nguyễn Hoàng Minh

28 tháng 10 2021

$Ư\left(30\right)=\left\{1;2;3;5;6;10;15;30\right\}\\ \Rightarrow x=5\left(B\right)\\ B\left(8\right)=\left\{0;8;16;24;32;...\right\}\\ \Rightarrow x=24\left(B\right)$

Đúng(2)

AT

An Trần

5 tháng 7 2016 - olm

BCNN của hai số tự nhiên bằng 770, một số bằng 14. Tìm số kia. Tìm hai số tự nhiên a và b, biết rằng :

a) ab = 360, [ a, b ] = 60

b) ( a, b ) = 12, [ a, b ] = 72

c) ( a, b ) = 6, [ a, b ] = 180

d) ( a, b ) = 15, [ a, b ] = 2100(a, b )

e) ab = 180, [ a, b ] = 20(a, b )

#Toán lớp 6

0

LK

Lâm Khánh Ly

12 tháng 8 2021

Tìm các số tự nhiên a biết :

a) (a+11) ⋮ (a+3) b) (a-3) ⋮ (a-14)

c) (2a+27) ⋮ (2a+1) d)(5a+28) ⋮ (a-2)

e) (3a-15) ⋮3 (a-14)

#Toán lớp 6

1

OY

OH-YEAH^^

12 tháng 8 2021

e) 3a-15⋮3.(a-14)

3a-15⋮3a-42

3a-42+27⋮3a-42

3a-42⋮3a-42 ⇒27⋮3a-42

3a-42∈Ư(27)

Ư(27)={1;-1;3;-3;9;-9;27;-27}

a∈{15;13;11;5}

Đúng(0)

TT

tran thi hien

2 tháng 4 2016 - olm

1,Tìm các số tự nhiên a,b,c,d,e biết a<<c<d<e và 1/a+1/b+1/c+1/d+1/e=1

2,Tìm x thuộc N biết:

1/3+1/6+1/10+...+2/x.(x+1)=1999/2001

#Toán lớp 6

0

LM

Lưu Minh Quân

27 tháng 10 2016 - olm

Câu hỏi hay

Cho các số tự nhiên >0 là a, b, c, d, e thỏa mãn tính chất a^2+b^2+c^2+d^2+e^2 là một số chia hết cho 2

Chứng tỏ rằng a+b+c+d+e là hợp số

#Toán lớp 6

6

LT

Le Thi Khanh Huyen

27 tháng 10 2016

Ta có :

$\left[\left(a+b\right)+\left(c+d\right)+e\right]^2$

$=\left(a+b\right)^2+\left(c+d\right)^2+e^2+2\left[\left(a+b\right)\left(c+d\right)+\left(a+b\right)e+\left(c+d\right)e\right]$

$=\left(a^2+b^2+c^2+d^2+e^2\right)+2ab+2cd+2\left[\left(a+b\right)\left(c+d\right)+\left(a+b\right)e+\left(c+d\right)e\right]$

$=\left(a^2+b^2+c^2+d^2+e^2\right)+2\left[ab+cd+\left(a+b\right)\left(c+d\right)+\left(a+b\right)e+\left(c+d\right)e\right]$

Do $2\left[ab+cd+\left(a+b\right)\left(c+d\right)+\left(a+b\right)e+\left(c+d\right)e\right]$chia hết cho 2 và $\left(a^2+b^2+c^2+d^2+e^2\right)$chia hết cho 2 nên $\left(a+b+c+d+e\right)^2$chia hết cho 2

$\Rightarrow a+b+c+d+e$chia hết cho 2

Đồng thời có $a+b+c+d+e>2$( Bắt buộc )

$\Rightarrow$a+b+c+d+e là hợp số

Bài này mình nhóm 3 số lại để trở thành hẳng đẳng thức đơn giản cho bạn dễ hiểu.

Đúng(0)

NV

ngô việt hoàng

28 tháng 10 2016

em lớp 6 nhìn bài giảng của chị CTV hoa hết cả mắt chẳng hiểu chi nổi.

em xin trình bày cách của em lập luận có gì thiếu sót chị chỉ bảo .

a^2+b^2+c^2+d^2+e^2 chia hết cho 2

* nếu a,b,c,d,e đều chẵn => hiển nhiên A=(a+b+c+d+e) là hợp số vì a,b,c,d,e>0

*nếu trong số (a,b,c,d,e) có số lẻ bình phương số lẻ là một số lẻ vậy do vậy số các con số lẻ phải chẵn

như vậy a+b+c+d+e cũng là một số chắn

mà a,b,c,d,e>0 do vậy a+b+c+d+e khác 2 vậy a+b+c+d+e=2k với k khác 1 => dpcm.

( ở đây em chỉ cần khác 2 loại số nguyên tố chẵn ) thực tế a+b+c+d+e >6)

Đúng(0)

TT

Thôi Trường Hoàn

12 tháng 9 2014 - olm

Giúp e câu hỏi này với m.n:

Bài 1: Tìm chữ số a,b,c (a,b,c là Số tự nhiên)

1)abcdeg.6=degabc

2)abc:11=a+b+c

Bài 2: Tìm chữ số a,b,c,d,e (a,b,c,d,e là Số tự nhiên)

1) (ab+cd).(ab-cd)=2002

2) 7abcd= 4.abcde7

#Toán lớp 6

1

TT

Thong the DEV

24 tháng 12 2018

Câu hỏi sai rùi nhé em

Đúng(0)

NH

Nguyễn Hà Ngọc Vân

30 tháng 7 2023

A/c giúp e chọn câu trả lời đúng và cách lm ạ. Câu 18: Tìm số tự nhiên x biết rằng 8(x-3) =0 A.x=1 B.x=3 C.x=2 D.x=4 Câu 19: Tìm số tự nhiên x biết:(5x-38):19=13 A.55 B.57 C.56 D.58

#Toán lớp 6

1