
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4\(\dfrac{1}{3}.\left(\dfrac{1}{6}-\dfrac{1}{2}\right)\)\(\le x\le\dfrac{2}{3}.\left(\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{3}{4}\right)\)
\(\dfrac{-13}{9}\le x\le\dfrac{-11}{12}\)
\(\dfrac{-468}{36}\le\dfrac{36.x}{36}\le\dfrac{-396}{36}\)
\(=>36.x\in\left\{-467;-466;-465;-464;...;-398;-397\right\}\)
\(=>x=-12\)

a)\(\left(\frac{1}{2}-\frac{1}{3}\right).6^x+6^{x+2}=6^{15}+6^{18}\)
\(\frac{1}{6}.6^x+6^{x+2}=6^{15}\left(1+6^3\right)\)
\(\frac{1}{6}.6^x\left(1+6^3\right)=6^{15}.217\)
\(6^{x-1}.217=6^{15}.217\)
\(6^{x-1}=6^{15}\)
\(x-1=15\)
\(x=16\)
b) \(\left(\frac{1}{2}-\frac{1}{6}\right).3^{x+4}-4.3^x=3^{16}-4.3^{13}\)
\(\frac{1}{3}.3^x.4\left(3^4-1\right)=3^{13}.4\left(3^3-1\right)\)
\(3^x.4.\left(3^3-1\right)=3^{13}.4.\left(3^3-1\right)\)
\(3^x=3^{13}\)
\(x=13\)
\(\left(\frac{1}{2}-\frac{1}{6}\right).\left(3^x.3^4\right)-4.3^x=3^{16}-4.3^{13}\)
=> \(\frac{1}{3}.3^x.3^4-4.3^x=3^{16}-4.3^{13}\)
=> \(3^x.3^4-4.3^x=\left(3^{16}-4.3^{13}\right):\frac{1}{3}\)
=> \(3^x.3^4-4.3^x=-386339074,3\)
=> \(3^x.\left(3^4-4\right)=-386339074,3\)
=> \(3^x.77=-386339074,3\)
=> \(3^x=-386339074,3:77\)
=> \(3^x=-5017390,575\)
=> x = ... chắc tự ngồi tính đc

a.\(\frac{1}{6}.6^x+6^x.36=6^{15}\left(1+6^3\right)\)
\(6^x.\frac{217}{6}=6^{15}.217\)
\(6^x=6^{16}\)
\(x=16\)

Mình chỉ làm được bài một thôi:
BÀI 1: Giải
Gọi ƯCLN(a;b)=d (d thuộc N*)
=> a chia hết cho d ; b chia hết cho d
=> a=dx ; b=dy (x;y thuộc N , ƯCLN(x,y)=1)
Ta có : BCNN(a;b) . ƯCLN(a;b)=a.b
=> BCNN(a;b) . d=dx.dy
=> BCNN(a;b)=\(\frac{dx.dy}{d}\)
=> BCNN(a;b)=dxy
mà BCNN(a;b) + ƯCLN(a;b)=15
=> dxy + d=15
=> d(xy+1)=15=1.15=15.1=3.5=5.3(vì x; y ; d là số tự nhiên)
TH 1: d=1;xy+1=15
=> xy=14 mà ƯCLN(a;b)=1
Ta có bảng sau:
| x | 1 | 14 | 2 | 7 |
| y | 14 | 1 | 7 | 2 |
| a | 1 | 14 | 2 | 7 |
| b | 14 | 1 | 7 | 2 |
TH2: d=15; xy+1=1
=> xy=0(vô lý vì ƯCLN(x;y)=1)
TH3: d=3;xy+1=5
=>xy=4
mà ƯCLN(x;y)=1
TA có bảng sau:
| x | 1 | 4 |
| y | 4 | 1 |
| a | 3 | 12 |
| b | 12 | 3 |
TH4:d=5;xy+1=3
=> xy = 2
Ta có bảng sau:
| x | 1 | 2 |
| y | 2 | 1 |
| a | 5 | 10 |
| b | 10 | 5 |
.Vậy (a;b) thuộc {(1;14);(14;1);(2;7);(7;2);(3;12);(12;3);(5;10);(10;5)}

\(3.\)
\(\frac{x-1}{2011}+\frac{x-2}{2010}+\frac{x-3}{2009}=\frac{x-4}{2008}\)
\(\Rightarrow\)\(\frac{x-1}{2011}-1+\frac{x-2}{2010}-1+\frac{x-3}{2009}-1-\frac{x-4}{2008}+1+2=0\)
\(\Rightarrow\)\(\frac{x-1}{2011}-\frac{2011}{2011}+\frac{x-2}{2010}-\frac{2010}{2010}+\frac{x-3}{2009}-\frac{2009}{2009}-\frac{x-4}{2008}+\frac{2008}{2008}=0\)
\(\Rightarrow\)\(\frac{x-2012}{2011}+\frac{x-2012}{2010}+\frac{x-2012}{2009}-\frac{x-2012}{2008}=0\)
\(\Rightarrow\)\(x-2012\left(\frac{1}{2011}+\frac{1}{2010}+\frac{1}{2009}+\frac{1}{2008}\right)=0\)
\(\Rightarrow\)\(x=2012\)

\(\left(\frac{1}{2}+\frac{3}{4}-\frac{1}{3}\right):\frac{-5}{6}< x< \frac{4}{21}.\frac{4}{7}\)
\(\Rightarrow\left(\frac{6}{12}+\frac{9}{12}-\frac{4}{12}\right):\frac{-10}{12}< x< \frac{16}{147}\)
\(\Rightarrow\frac{11}{12}.\frac{-12}{10}< x< \frac{16}{147}\)
\(\Rightarrow\frac{-11}{10}< x< \frac{16}{147}\)
\(\Rightarrow\frac{-1617}{1470}< x< \frac{16}{1470}\)
\(x=\left\{-1;0\right\}\)
Ta có: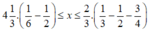
Suy ra : x = -1