Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(x^{-4}+x^{\frac{5}{2}}\right)^{12}\) có SHTQ: \(C_{12}^kx^{-4k}.x^{\frac{5}{2}\left(12-k\right)}=C^k_{12}x^{30-\frac{13}{2}k}\)
Số hạng chứa \(x^8\Rightarrow30-\frac{13}{2}k=8\Rightarrow\) ko có k nguyên thỏa mãn
Vậy trong khai triển trên ko có số hạng chứa \(x^8\)
b/ \(\left(1-x^2+x^4\right)^{16}\)
\(\left\{{}\begin{matrix}k_0+k_2+k_4=16\\2k_2+4k_4=16\end{matrix}\right.\)
\(\Rightarrow\left(k_0;k_2;k_4\right)=\left(8;8;0\right);\left(9;6;1\right);\left(10;4;2\right);\left(11;2;3\right);\left(12;0;4\right)\)
Hệ số của số hạng chứa \(x^{16}\):
\(\frac{16!}{8!.8!}+\frac{16!}{9!.6!}+\frac{16!}{10!.4!.2!}+\frac{16!}{11!.2!.3!}+\frac{16!}{12!.4!}=...\)
c/ SHTQ của khai triển \(\left(1-2x\right)^5\) là \(C_5^k\left(-2\right)^kx^k\)
Số hạng chứa \(x^4\) có hệ số: \(C_5^4.\left(-2\right)^4\)
SHTQ của khai triển \(\left(1+3x\right)^{10}\) là: \(C_{10}^k3^kx^k\)
Số hạng chứa \(x^3\) có hệ số \(C_{10}^33^3\)
\(\Rightarrow\) Hệ số của số hạng chứa \(x^5\) là: \(C_5^4\left(-2\right)^4+C_{10}^3.3^3\)

Số hạng thứ 5 trong khai triển
![]()
Nhận xét. Học sinh có thể nhầm số hạng thứ 5 ứng với k=5 nên là
![]()
Hoặc tính nhầm dẫn đến chọn A, hoặc chọn C
Chọn B

Ta có: (x3 + )8=
Ck8 x3(8 – k) (
)k =
Ck8 x24 – 4k
Trong tổng này, số hạng Ck8 x24 – 4k không chứa x khi và chỉ khi
⇔ k = 6.
Vậy số hạng không chứa x trong khai triển (theo công thức nhị thức Niu - Tơn) của biểu thức đã cho là C68 = 28.

\(\left(x+2.x^{-1}\right)^{10}\)
Số hạng tổng quát: \(C_{10}^k.x^k.\left(2x^{-1}\right)^{10-k}=C_{10}^k.2^{10-k}.x^{2k-10}\)
Số hạng chứa \(x^2\Rightarrow2k-10=2\Rightarrow k=6\)
Hệ số: \(C_{10}^6.2^4=3360\)

\(\left(x^{-\frac{2}{3}}+x^{\frac{3}{4}}\right)^{17}=\sum\limits^{17}_{k=0}C_{17}^k\left(x^{-\frac{2}{3}}\right)^k\left(x^{\frac{3}{4}}\right)^{17-k}=\sum\limits^{17}_{k=0}C_{17}^kx^{\frac{51}{4}-\frac{17}{12}k}\)
Số hạng thứ 13 \(\Rightarrow k=12\) là: \(C_{17}^{12}x^{-\frac{17}{4}}\)
b/ Xét khai triển:
\(\left(3-x\right)^n=C_n^03^n+C_n^13^{n-1}\left(-x\right)^1+C_n^23^{n-2}\left(-x\right)^2+...+C_n^n\left(-x\right)^n\)
Cho \(x=1\) ta được:
\(2^n=3^nC_n^0-3^{n-1}C_n^1+3^{n-2}C_n^2+...+\left(-1\right)^nC_n^n\)
À, đến đây mới thấy đề thiếu, biết rằng cái kia làm sao hả bạn?

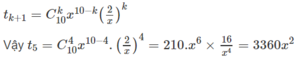
Số hạng thứ \(k+1\) trong khai triển là :
\(t_{k+1}=C^k_{10}x^{10-k}\left(\dfrac{2}{x}\right)^k\)
Vậy \(t_5=C^4_{10}x^{10-4}.\left(\dfrac{2}{x}\right)^4=210.x^6.\dfrac{16}{x^4}=3360x^2\)