DN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
25 tháng 3 2017
Các số có căn bậc hai:
a = 0 c = 1 d = 16 + 9
e = 32 + 42 h = (2-11)2 i = (-5)2
l = √16 m = 34 n = 52 - 32
Căn bậc hai không âm của các số đó là:
PT
1
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
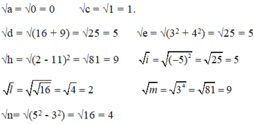
a) \(\sqrt {15} \) đọc là: căn bậc hai số học của mười lăm
\(\sqrt {27,6} \) đọc là: căn bậc hai số học của hai mươi bảy phẩy sáu
\(\sqrt {0,82} \) đọc là: căn bậc hai số học của không phẩy tám mươi hai
b) Căn bậc hai số học của 39 viết là: \(\sqrt {39} \)
Căn bậc hai số học của \(\frac{9}{{11}}\) viết là: \(\sqrt {\frac{9}{{11}}} \)
Căn bậc hai số học của \(\frac{{89}}{{27}}\) viết là: \(\sqrt {\frac{{89}}{{27}}} \)
10 tháng 10 2021
\(\sqrt{2}\approx1.4142\)
\(\sqrt{5}=2.236\)
\(\sqrt{9}=3\)
\(\sqrt{36}=6\)
\(\sqrt{-7}=\varnothing\)
CM
14 tháng 3 2017
a= 2 là căn bậc hai của 4
b = -5 là căn bậc hai của 25;
c = 1 là căn bậc hai của 1
d = 25 là căn bậc hai của 625
e = 0 là căn bậc hai của 0;
g = √7 là căn bậc hai của 7;
h = 3/4 là căn bậc hai của 9/16
i= √4 -3 = 2-3 =-1 là căn bậc hai của 1
PN
27 tháng 7 2017
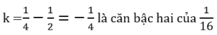
Một số không âm mới có căn bậc hai.
Vậy trong các số đã cho, các số có căn bậc hai là \(0;3^2+4^2;5^2-4^2;\left(-5\right)^2\)
Căn bậc hai của chúng là:
- Với số \(0\): \(\sqrt{0}=0\)
- Với số \(3^2+4^2=9+16=25=5^2\)
nên \(\sqrt{3^2+4^2}=5;-\sqrt{3^2+4^2}=-5\)
- Với số \(5^2-4^2=25-16=9=3^2\)
nên \(\sqrt{5^2-4^2}=3;-\sqrt{5^2-4^2}=-3\)
- Với số \(\left(-5\right)^2=25=5^2\)
nên \(\sqrt{\left(-5\right)^2}=5;-\sqrt{\left(-5\right)^2}=-5\)
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
a) Vì 0,8 > 0 và \(0,{8^2} = 0,64\) nên số 0,8 là căn bậc hai số học của số 0,64
b) Vì tuy \({( - 11)^2} = 121\) nhưng -11 < 0 nên số -11 không phải là căn bậc hai số học của số 121
c) Vì \(1,{4^2} = 1,96\) và 1,4 > 0 nên số 1,4 là căn bậc hai số học của số 1,96
Nhưng vì -1,4 < 0 nên –1,4 không phải là căn bậc hai số học của số 1,96.