Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^3+2x^2\left(4y-1\right)-4xy^2-9y^3-f\left(x\right)=-5x^3+8x^2y-4xy^2-9y^3\\ \Rightarrow\left(x^3+8x^2y+2x^2-4xy^2-9y^3\right)-f\left(x\right)=-5x^3+8x^2y-4xy^2-9y^3\\ \Rightarrow f\left(x\right)=x^3+8x^2y+2x^2-4xy^2-9y^3+5x^3-8x^2y+4xy^2+9y^3\\ \Rightarrow f\left(x\right)=6x^3+2x^2\)

a, \(\frac{x}{4}=\frac{y}{5}\Rightarrow\frac{3.y}{3.5}=\frac{2.x}{2.4}\Rightarrow\frac{3y}{15}=\frac{2x}{8}\)
Áp dụng tính chất của Dãy tỷ số :
\(\frac{3y}{15}=\frac{2x}{8}\Rightarrow\frac{3y-2x}{15-8}=\frac{14}{7}=2\)
\(\frac{x}{4}=2\Rightarrow x=8\)
\(\frac{y}{5}=2\Rightarrow y=10\)
b, ta có :
\(\frac{x}{2}=\frac{y}{3}\)
đặt \(\frac{x}{2}=\frac{y}{3}=k\)
\(\Leftrightarrow x=2k;y=3k\)
\(\Rightarrow xy=2k.3k=6k^2\)
\(\Rightarrow96=6k^2\Rightarrow k^2=16\Rightarrow k=\pm4\)
TH1 : \(k=4\Rightarrow x=4.2=8;y=4.3=12\)
TH2 : \(k=-4\Rightarrow x=-4.2=-8;y=-4.3=-12\)
.................


Ta có : a song song với b
=> Góc A = Góc B = 90độ
Hay x = 90 độ
=> Góc D + Góc C = 180độ ( 2 góc trong cùng phía )
=> y + 130 độ = 180 độ
=> y = 50 độ
Vẽ Cx song song với Am(1), ta được :
=> Góc mAC + Góc ACx = 180 độ
=> Góc mAC + Góc BCA + Góc BCx = 180 độ
Hay Góc BCx = 180 độ - 45 độ - 60 độ = 75 độ
Vì Góc nBC + Góc BCx = 180 độ ( 75 độ + 105 độ = 180 độ )
Mà Góc nBC và Góc BCx là 2 góc trong cùng phía
Nên ta được Bn song song với Cx (2)
Từ (1) và (2) => Bn song song với Am

Câu 4:
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Câu 1:
\(a,=\dfrac{1}{2}+9\cdot\dfrac{1}{9}-18=\dfrac{1}{2}+1-18=-\dfrac{33}{2}\\ b,=2-1+4\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{9}\cdot9=1+1+9=11\\ c,=-21,3\left(54,6+45,4\right)=-21,3\cdot100=-2130\\ d,B=\left(\dfrac{1}{16}+\dfrac{1}{2}-\dfrac{1}{16}\right):\left(\dfrac{1}{8}-\dfrac{1}{8}+1\right)=\dfrac{1}{2}:1=\dfrac{1}{2}\)

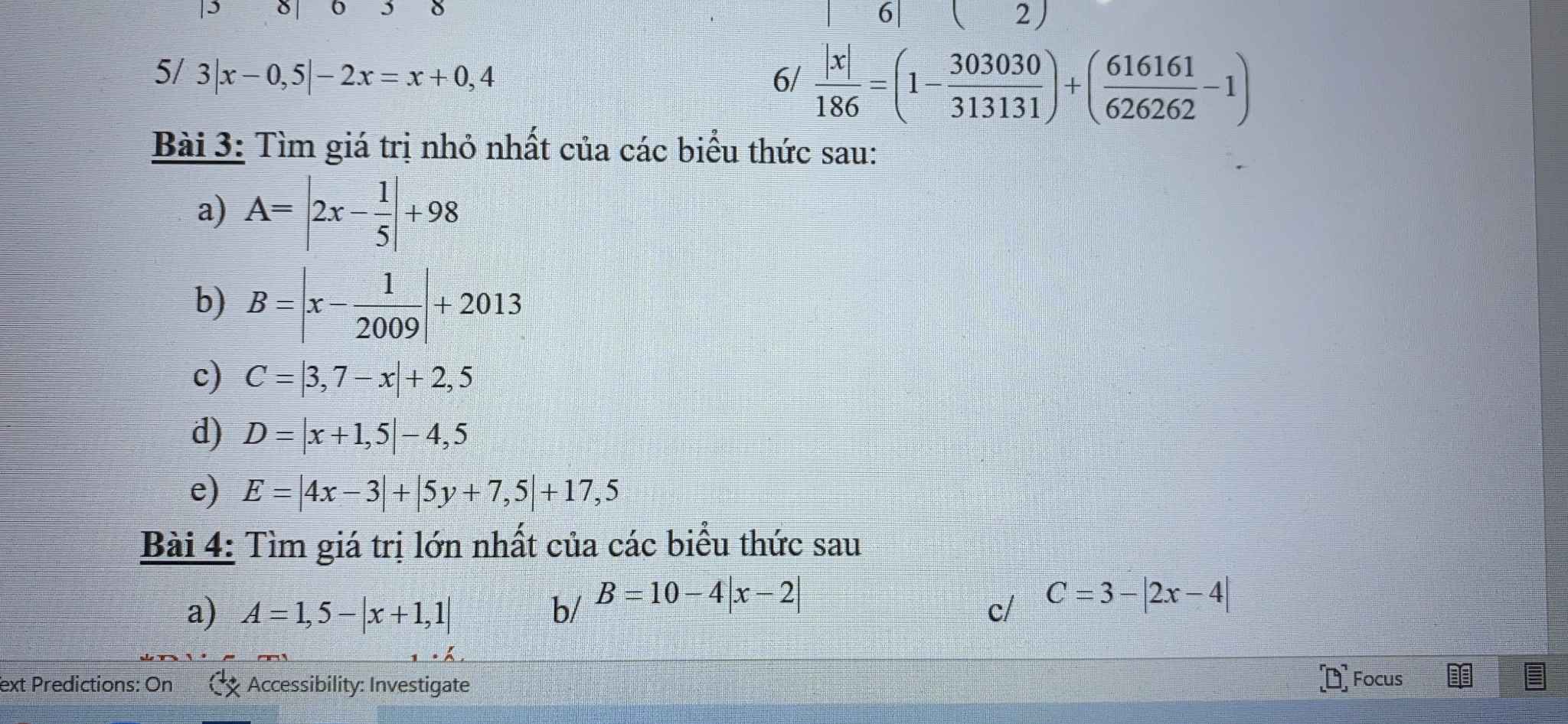
Bài 4:
a: Ta có: \(-\left|x+1.1\right|\le0\forall x\)
\(\Leftrightarrow-\left|x+1.1\right|+1.5\le1.5\forall x\)
Dấu '=' xảy ra khi x=-1,1
b: Ta có: \(-4\left|x-2\right|\le0\forall x\)
\(\Leftrightarrow-4\left|x-2\right|+10\le10\forall x\)
Dấu '=' xảy ra khi x=2
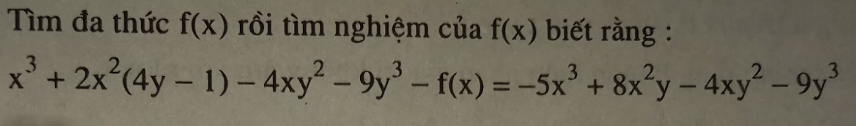
 giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !
giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !

ta có góc \(\widehat{FEB}+\widehat{EBC}=180^0\text{ mà hai học này ở vị trí trong cùng phía nên }\)BC song song với EF
nên \(x=\widehat{FCB}=\widehat{CFE}=50^0\)