ND
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LQ
3 tháng 11 2018
phàn dưới mik chép thiếu nha, đề bài đầy đủ là
tìm số nguyên tố p sao cho p+4, p+6, p+10, p+12, p+16 cũng là số nguyên tố
NN
4
30 tháng 7 2017
a) p, p+2, p+4 nguyên tố?
*nếu p = 3 => p+2 = 5, p+4 = 7 là 3 số nguyên tố
*p # 3:
nếu p chia 3 dư 1 => p+2 chia hết cho 3 : ko là số nguyên tố
nếu p chia 3 dư 2 => p+4 chia hết cho 3 : ko là số nguyên tố
Vậy chỉ có số nguyên tố p duy nhất thỏa là p = 3
b) p+2; p+6;p+8;p+14 nguyên tố
đặt: p = 5k+r (0 ≤ r < 5)
* nếu r = 1 => p+14 = 5k+15 chia hết cho 5
* nếu r = 2 => p+8 = 5k + 10 chia hết cho 5
* nếu r = 3 => p+2 = 5k+5 chia hết cho 5
* nếu r = 4 => p+6 = 5k+10 chia hết cho 5
* nếu r = 0 => p = 5k là nguyên tố khi k = 1
p = 5, các số kia là: 7,11,13,19 là các số nguyên tố: thỏa
Vậy p = 5
c) p+6, p+8, p+12, p+14 nguyên tố
p = 5k+r
xét như trên thấy r không thể là 1, 2, 3,4
r = 0 => p = 5k nguyên tố => p = 5
các số là 5, 11,13,17,19 nguyên tố
Vậy p = 5
30 tháng 7 2017
❤nguyen ngoc nam❤
a) p, p+2, p+4 nguyên tố?
*nếu p = 3 => p+2 = 5, p+4 = 7 là 3 số nguyên tố
*p # 3:
nếu p chia 3 dư 1 => p+2 chia hết cho 3 : ko là số nguyên tố
nếu p chia 3 dư 2 => p+4 chia hết cho 3 : ko là số nguyên tố
Vậy chỉ có số nguyên tố p duy nhất thỏa là p = 3
b) p+2; p+6;p+8;p+14 nguyên tố
đặt: p = 5k+r (0 ≤ r < 5)
* nếu r = 1 => p+14 = 5k+15 chia hết cho 5
* nếu r = 2 => p+8 = 5k + 10 chia hết cho 5
* nếu r = 3 => p+2 = 5k+5 chia hết cho 5
* nếu r = 4 => p+6 = 5k+10 chia hết cho 5
* nếu r = 0 => p = 5k là nguyên tố khi k = 1
p = 5, các số kia là: 7,11,13,19 là các số nguyên tố: thỏa
Vậy p = 5
c) p+6, p+8, p+12, p+14 nguyên tố
p = 5k+r
xét như trên thấy r không thể là 1, 2, 3,4
r = 0 => p = 5k nguyên tố => p = 5
các số là 5, 11,13,17,19 nguyên tố
Vậy p = 5
UO
6
4 tháng 7 2021
P=1 nha. Minh thử và làm lại rồi nha. Đúng 100%
6I
1 tháng 12 2017
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
H9
HT.Phong (9A5)
CTVHS
28 tháng 10 2023
Bài 18:
Ta có:
\(2015^{2015}-2015^{2014}=2015^{2014}\cdot\left(2015-1\right)=2015^{2014}\cdot2014\)
\(2015^{2016}-2015^{2015}=2015^{2015}\cdot\left(2015-1\right)=2015^{2015}\cdot2014\)
Mà: \(2014< 2015\)
\(\Rightarrow2015^{2014}< 2015^{2015}\)
\(\Rightarrow2015^{2014}\cdot2014< 2015^{2015}\cdot2014\)
\(\Rightarrow2015^{2015}-2015^{2014}< 2015^{2016}-2015^{2015}\)
Vậy: ...
1 tháng 11 2015
Bài 2 : c)
+Nếu p = 2 ⇒ p + 2 = 4 (loại)
+Nếu p = 3 ⇒ p + 6 = 9 (loại)
+Nếu p = 5 ⇒ p + 2 = 7, p + 6 = 11, p + 8 = 13, p + 12 = 17, p + 14 = 19 (thỏa mãn)
+Nếu p > 5, ta có vì p là số nguyên tố nên ⇒ p không chia hết cho 5 ⇒ p = 5k+1, p = 5k+2, p = 5k+3, p = 5k+4
-Với p = 5k + 1, ta có: p + 14 = 5k + 15 = 5 ( k+3) ⋮ 5 (loại)
-Với p = 5k + 2, ta có: p + 8 = 5k + 10 = 5 ( k+2 ) ⋮ 5 (loại)
-Với p = 5k + 3, ta có: p + 12 = 5k + 15 = 5 ( k+3) ⋮ 5 (loại)
-Với p = 5k + 4, ta có: p + 6 = 5k + 10 = 5 ( k+2) ⋮ 5 (loại)
⇒ không có giá trị nguyên tố p lớn hơn 5 thỏa mãn
Vậy p = 5 là giá trị cần tìm
Bài 4 : Tích của hai số tự nhiên là số nguyên tố nên một số là 1, số còn lại (kí hiệu a) là số nguyên tố.
Theo đề bài, 1 + a cũng là số nguyên tố. Xét hai trường hợp :
- Nếu 1 + a là số lẻ thì a là số chẵn. Do a là ....
Còn lại bạn tự làm nha , mình mỏi tay quá !
13 tháng 8 2021
Câu b:
Đến đoạn này cũng xét như câu a
Câu c:
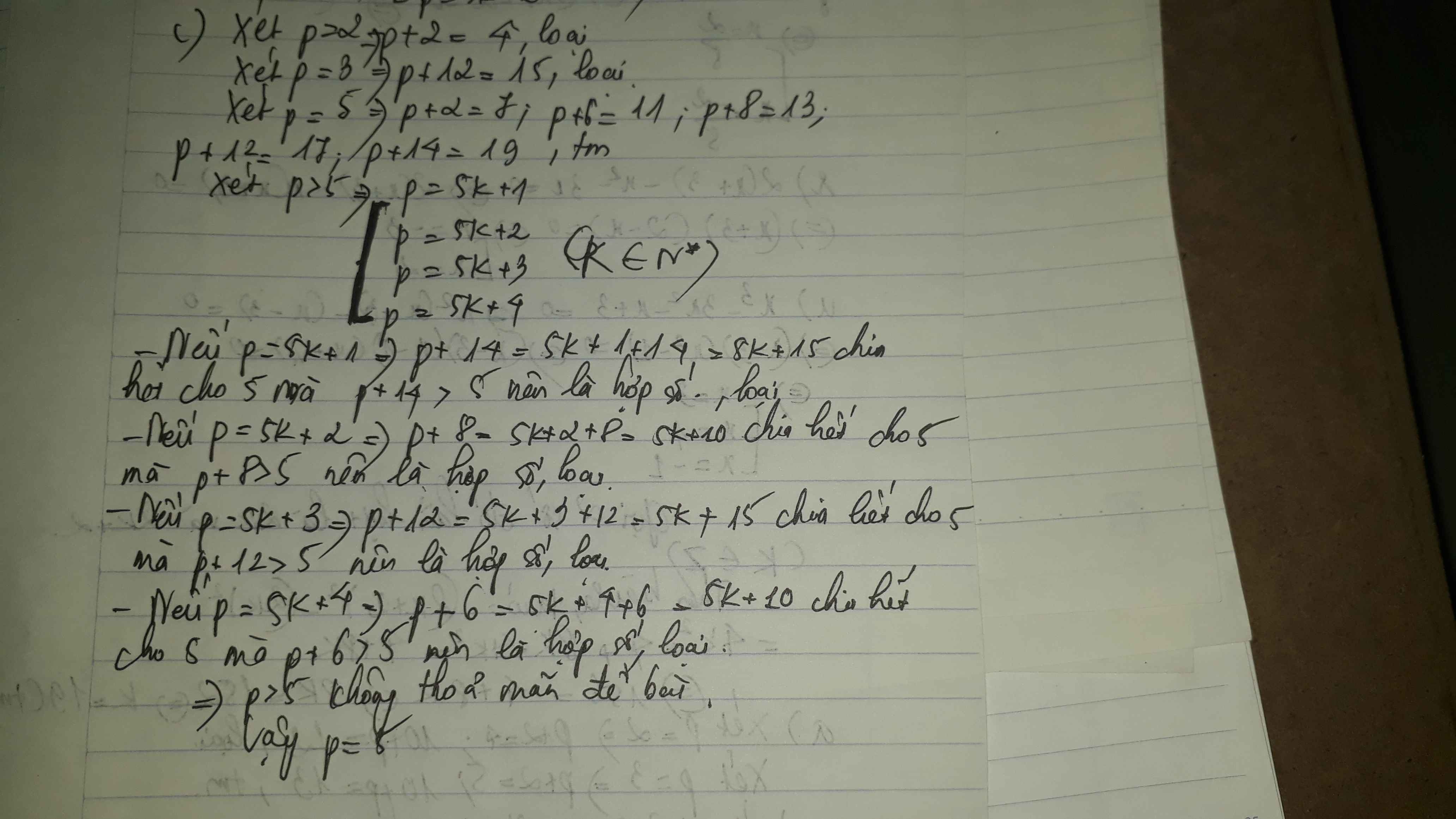
- Nếu p = 2 => p + 4 = 6 => hợp số (loại)
- Nếu p = 3 => p + 6 = 9 => hợp số (loại)
- Nếu p = 5 => p + 4 = 9 => hợp số (loại)
- Nếu p = 7 => p + 4 = 11 ; p + 6 = 13 ; p + 10 = 17 ; p + 12 = 19 ; p + 16 = 23 ; p + 22 = 29 => số nguyên tố (thỏa mãn)
- Nếu p > 7 => p không chia hết cho 7
+) Nếu p = 7k + 1 => p + 6 = 7k + 1 + 6 = 7k + 7 => hợp số (loại)
+) Nếu p = 7k + 2 => p + 12 = 7k + 2 + 12 = 7k + 14 => hợp số (loại)
+) Nếu p = 7k + 3 => p + 4 = 7k + 3 + 4 = 7k + 7 => hợp số (loại)
+) Nếu p = 7k + 4 => p + 10 = 7k + 4 + 10 = 7k + 14 => hợp số (loại)
+) Nếu p = 7k + 5 => p + 16 = 7k + 5 + 16 = 7k + 21 => hợp số (loại)
+) Nếu p = 7k + 6 => p + 22 = 7k + 6 + 22 = 7k + 28 => hợp số (loại)
Vậy p = 7
bạn ST sai rồi p=1
p+4=5
p+6=7
p+10=11
p+12=13
p+16=17
p+22=23
\(\Leftrightarrow\)tất cả đều là số nguyên tố
Chúc các bạn học giỏi