Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có
\(y'=\left(cosx-sinx\right)e^x+\left(sinx+cosx\right)e^x=2.cosx.e^x\)

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

cos2x+5=2.(2−cosx)(sinx−cosx)cos2x+5=2.(2−cosx)(sinx−cosx)
⇔2.cos2x−1+5=2.(2.sinx−2.cosx−cosx.sinx+cos2x)⇔2.cos2x−1+5=2.(2.sinx−2.cosx−cosx.sinx+cos2x)
⇔cos2x+2=2.sinx−2.cosx−cosx.sinx+cos2x⇔cos2x+2=2.sinx−2.cosx−cosx.sinx+cos2x
⇔2.(sinx−cosx)−cosx.sinx=2⇔2.(sinx−cosx)−cosx.sinx=2
Đặt t=sinx−cosxt=sinx−cosx , khi đó ta có t2−12=(−cosx.sinx)t2−12=(−cosx.sinx)
pt ⇔2.t+t2−12=2⇔2.t+t2−12=2

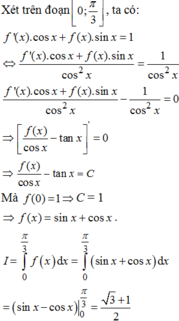

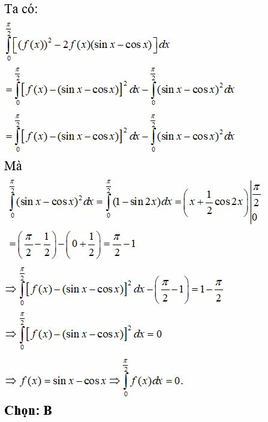

Chọn A