Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:
Đáp án C
Trên khoảng ( a, b )ta có: f ' (x)< 0 nên hàm số nghịch biến trên khoảng (a, b)
Ta có f (a) > f (b)
Tương tự trên khoảng ( b,c ) có f ' ( x ) > 0 nên hàm số đồng biến trên ( b,c )suy ra f (c) > f (b)
(Đến đây rõ ràng ra suy ra được 4 đúng và 1 trong 2 ý (1) và (2) có 1 ý đúng ta sẽ suy ra đáp án cần chọn là C)
Chặt chẽ hơn: Dựa vào đồ thị ta thấy
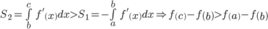Do đó f (c) > f (a) > f (b)
Đáp án D
Điều kiện cần để x 0 là điểm cực trị của hàm số f ( x ) là f ' ( x 0 ) = 0
Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B
Đáp án C
x n = x . x .... x ⏟ n s o n ≥ 1 đúng; 2 x − 1 0 = 1 sai khi x = 1 2
4 x + 1 − 2 = 1 4 x + 1 2 sai khi x = − 1 4 ; x − 1 1 3 + 5 − x 1 2 = 2 ⇔ x − 1 3 + 5 − x = 2 Sai: ví dụ x = 1 là nghiệm của phương trình x − 1 3 + 5 − x = 2 nhưng không là nghiệm của PT x − 1 1 3 + 5 − x 1 2 = 2.
