Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Đặt t = cos x ⇒ t ∈ − 1 ; 1 ⇒ y = f t = 2 t + 1 t − m
Ta có f ' t = 2 m + 1 t − m 2 sin x
Hàm số đồng biến trên khoảng:
0 ; π ⇒ f ' t > 0 t − m ≠ 0 ⇔ 2 m + 1 sinx > 0 m ≠ t ⇔ m > − 1 2 m ≥ 1 m ≤ − 1 ⇒ m ≥ 1

Đáp án D
Đặt t = c osx ⇒ t'=-sinx < 0 ; ∀ x ∈ 0 ; π suy ra t ∈ − 1 ; 1 .
Khi đó
y = f t = 2 t + 1 t − m ⇒ f ' t = − 2 m + 1 t − m 2 x t ' .
Hàm số đã cho đồng biến trên khoảng 0 ; π
⇔ f ' t > 0 ; ∀ t ∈ − 1 ; 1 ⇔ − 2 m + 1 t − m 2 x t ' > 0 ; ∀ t ∈ − 1 ; 1
mà t ' < 0 suy ra
2 m + 1 t − m 2 > 0 ; ∀ t ∈ − 1 ; 1 .
⇔ 2 m + 1 > 0 t = m ∉ − 1 ; 1 ⇔ m > − 1 2 m ∉ − 1 ; 1 ⇔ m > − 1 2 1 2 ≥ 1 m ≤ − 1 ⇔ m ≥ 1 là giá trị cần tìm

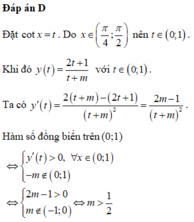
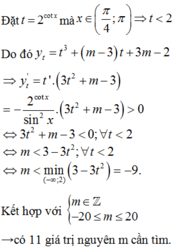


Đáp án B
Xét hàm số
y = 2 cot x + 1 cot x + m → t = cot x y = 2 t + 1 t + m ⇒ y t ' = t ' . 2 m − 1 t + m 2
Để hàm số đã cho đồng biến trên
π 4 ; π 2 ⇔ y t ' > 0 , ∀ x ∈ 0 ; 1 ⇔ t ' . 2 m − 1 t + m 2 > 0 , ∀ x ∈ 0 ; 1
Mà
t ' < 0 , ∀ x ∈ 0 ; 1 ⇒ 2 m − 1 t + m 2 < 0 ; ∀ x ∈ 0 ; 1 ⇔ 2 m − 1 < 0 t = − m ∉ 0 ; 1 ⇔ m < 1 2 − m ≥ 1 − m ≤ 0 ⇔ m ≤ − 1 0 ≤ m < 1 2