

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!

Đáp án B
Hàm số có tiệm cận đứng là x=-m để tiệm cận này đi qua M 3 ; 1 ⇒ − m = 3 ⇒ m = − 3

Đáp án C
Phương pháp :
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2
y = f’(m – 2)(x – m +2)+y(m – 2) (d)
+) Xác định các giao điểm của d và các đường tiệm cận => x2;y1
+) Thay vào phương trình x2 + y1 = –5 giải tìm các giá trị của m.
Cách giải: TXĐ: D = R\ {–2}
Ta có 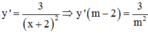
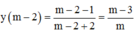
=>Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2 là: 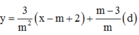
Đồ thị hàm số y = x - 1 x + 2 có đường TCN y = 1và tiệm cậm đứng x = –2
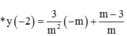
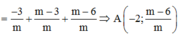
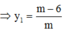
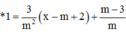
![]()
![]()
![]()
![]()
![]()
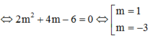
![]()

Đáp án A
![]()
hơn bậc mẫu), nên đồ thị hàm số luôn có đúng một tiệm cận ngang là y = 0, với mọi giá trị của m. Tiệm cận ngang này không đi qua điểm A(-1;2)
Vậy ta phải tìm m sao cho đồ thị hàm số có một tiệm cận đứng đi qua điểm A(-1;2), đó là x = 1
Đồ thị hàm số có tiệm cận đứng là x = 1
