K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TD
1
18 tháng 12 2022
\(\overrightarrow{AB}=\left(1;2\right)\)
\(\overrightarrow{AC}=\left(x;y+5\right)\)
Để A,B,C thẳng hàng thì x/1=y+5/2
=>2x=y+5
=>y=2x-5
24 tháng 9 2023
Tham khảo:
a) Ta có: \(\overrightarrow b = \left( {4; - 1} \right)\) và \(\overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j \;\; \Rightarrow \;\overrightarrow a \;\left( {3; - 2} \right)\)
\( \Rightarrow 2\;\overrightarrow a - \overrightarrow b = \left( {2.3 - 4\;;\;2.\left( { - 2} \right) - \left( { - 1} \right)} \right) = \left( {2; - 3} \right)\)
Lại có: M (-3; 6), N(3; -3)
\( \Rightarrow \overrightarrow {MN} = \left( {3 - \left( { - 3} \right); - 3 - 6} \right) = \left( {6; - 9} \right)\)
Dễ thấy:\(\left( {6; - 9} \right) = 3.\left( {2; - 3} \right)\) \( \Rightarrow \overrightarrow {MN} = 3\left( {2\;\overrightarrow a - \overrightarrow b } \right)\)
b) Ta có: \(\overrightarrow {OM} = \left( { - 3;6} \right)\) ( do M(-3; 6)) và \(\overrightarrow {ON} = \left( {3; - 3} \right)\) (do N (3; -3)).
Hai vectơ này không cùng phương (vì \(\frac{{ - 3}}{3} \ne \frac{6}{{ - 3}}\)).
Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
c) Các điểm O, M, N không thẳng hàng nên OMNP là một hình hành khi và chỉ khi \(\overrightarrow {OM} = \overrightarrow {PN} \).
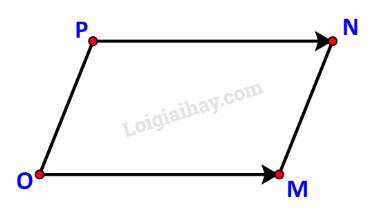
Do \(\overrightarrow {OM} = \left( { - 3;6} \right),\;\overrightarrow {PN} = \left( {3 - x; - 3 - y} \right)\) nên
\(\overrightarrow {OM} = \overrightarrow {PN} \Leftrightarrow \left\{ \begin{array}{l} - 3 = 3 - x\\6 = - 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = - 9\end{array} \right.\)
Vậy điểm cần tìm là P (6; -9).
1 tháng 10 2020
ycbt\(\Leftrightarrow\hept{\begin{cases}9^4a+9^3b+9^2c+9d+e=32078\left(p\right)\\a,b,c,d,e\in N;\le8;a\ne0\end{cases}}\)
VP(p): 9 dư 2 =>e =2
\(\Rightarrow9^3a+9^2b+9c+d=\frac{32078-2}{9}=4564⋮9\Rightarrow d=0\)
\(\Rightarrow9^2a+9b+c=\frac{3564}{9}=396⋮9\Rightarrow c=0\)
\(\Rightarrow9a+b=\frac{396}{9}=44\)chia 9 dư 8 => b=8
=> 9a=36=>a=4
Vậy S =14
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) Tam giác BDC vuông tại C nên \(\sin \widehat {BDC} = \frac{{BC}}{{BD}} = \frac{a}{{2R}}.\)
b)
TH1: Tam giác ABC có góc A nhọn
\(\widehat {BAC} = \widehat {BDC}\) do cùng chắn cung nhỏ BC.
\( \Rightarrow \sin \widehat {BAC} = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
TH2: Tam giác ABC có góc A tù
\(\widehat {BAC} + \widehat {BDC} = {180^o}\) do ABDC là tứ giác nội tiếp (O).
\( \Rightarrow \sin \widehat {BAC} = \sin ({180^o} - \widehat {BAC}) = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
Vậy với góc A nhọn hay tù ta đều có \(2R = \frac{a}{{\sin A}}.\)
b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O).
Khi đó ta có: \(\sin A = \sin {90^o} = 1\) và \(a = BC = 2R\)
Do đó ta vẫn có công thức: \(2R = \frac{a}{{\sin A}}.\)
11 tháng 12 2020
Ủa phải là vt a ⊥ vt b chứ tao hong thì góc giữa chúng là 90 độ ròi
12 tháng 1 2021
Theo định lí Viet thì \(\left\{{}\begin{matrix}x_1+x_2=4m\\x_1.x_2=\left(3m-3\right)^2\end{matrix}\right.\)
\(\dfrac{16}{9}.x_1.x_2=\dfrac{16}{9}.\left(3m-3\right)^2\)
⇒ \(\dfrac{16}{9}.x_1.x_2=\left[\dfrac{4}{3}.\left(3m-3\right)\right]^2\)
⇒ \(\dfrac{16}{9}.x_1.x_2=\left(4m-4\right)^2\)
⇒ \(\dfrac{16}{9}.x_1.x_2=\left(x_1+x_2-4\right)^2\)
Đối chiếu ⇒ \(\left\{{}\begin{matrix}a=-4\\b=\dfrac{16}{9}\end{matrix}\right.\)
⇒ \(\dfrac{b}{a}=\dfrac{-4}{9}\)
CM
8 tháng 3 2019
Vậy 
là vec tơ cùng hướng với 
và có độ dài 
Vậy 
là vec tơ ngược hướng với 
và có độ dài 
(Do hai vec tơ 
không cùng phương nên chỉ bằng nhau khi chúng đồng thời bằng 0→).
Vậy MN song song với BC khi và chỉ khi α = β.
\(\Leftrightarrow\left[{}\begin{matrix}a+b>a-b\\a+b< -a+b\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}b>0\\a< 0\end{matrix}\right.\)