Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì \(2a=5b\) nên \(\dfrac{a}{5}=\dfrac{b}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{3a+4b}{3.5+2.4}=\dfrac{46}{23}=2\)
\( \Rightarrow a=2.5=10;\\b=2.2=4\)
Vậy \(a = 10 ; b = 4\)
b) Vì a : b : c = 2 : 4 : 5
\( \Rightarrow \dfrac{a}{2} = \dfrac{b}{4} = \dfrac{c}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\( \Rightarrow \dfrac{a}{2} = \dfrac{b}{4} = \dfrac{c}{5}= \dfrac{{a + b - c}}{{2 + 4 - 5}}= \dfrac{3}{1}=3\)
\( \Rightarrow a = 3.2=6;\\b = 3.4=12;\\c =3.5=15.\)
Vậy \(a=6;b=12;c=15\).

Theo đề, ta có:
\(\left\{{}\begin{matrix}\dfrac{a}{5}=\dfrac{b}{7}\\\dfrac{b}{5}=\dfrac{c}{3}\end{matrix}\right.\Leftrightarrow\dfrac{a}{25}=\dfrac{b}{35}=\dfrac{c}{21}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{25}=\dfrac{b}{35}=\dfrac{c}{21}=\dfrac{2a-b+c}{2\cdot25-35+21}=\dfrac{114}{36}=\dfrac{19}{6}\)
Do đó: a=475/6; b=665/6; c=133/2

\(\frac{a}{4}=\frac{b}{7};5b=3c\Rightarrow\frac{b}{3}=\frac{c}{5}\)
\(\frac{a}{12}=\frac{b}{21}=\frac{c}{35}=\frac{2a-b+c}{2.12-21+35}=\frac{14}{38}=\frac{7}{19}\)
\(a=\frac{7}{19}.12=\frac{84}{19}\)
\(b=\frac{7}{19}.21=\frac{147}{19}\)
\(c=\frac{7}{19}.35=\frac{245}{19}\)

a. ta có : \(\begin{cases}\frac{a}{b}=\frac{1}{2}\\\frac{a}{c}=\frac{2}{5}\\2a-b+c=7\end{cases}\) \(\Leftrightarrow\begin{cases}b=2a\\a=\frac{2}{5}c\\b-b+c=7\end{cases}\) \(\Leftrightarrow\begin{cases}b=2a\\a=\frac{2}{5}c\\c=7\end{cases}\) \(\Leftrightarrow\begin{cases}a=\frac{14}{5}\\b=\frac{28}{5}\\c=7\end{cases}\)
b. \(\begin{cases}2c=4a\\2b=3a\\a^2-b^2+2c^2=108\end{cases}\) \(\Leftrightarrow\begin{cases}c=2a\\b=\frac{3}{2}a\\a^2-b^2+2c^2=108\end{cases}\) \(\Leftrightarrow\begin{cases}c=2a\\b=\frac{3}{2}a\\a^2-\left(\frac{3}{2}a\right)^2+2\left(2a\right)^2=108\left(1\right)\end{cases}\)
Giải (1) ta có : a=4 hoặc a = -4
Với a=4 thì : \(\begin{cases}a=4\\b=6\\c=8\end{cases}\)
Với a=-4 thì : \(\begin{cases}a=-4\\b=-6\\c=-8\end{cases}\)

Có : \(\frac{a}{4}=\frac{b}{7}\Rightarrow\frac{a}{12}=\frac{b}{21}\)(1)
\(5b=3c\Rightarrow\frac{b}{3}=\frac{c}{5}\Rightarrow\frac{b}{21}=\frac{c}{35}\) (2)
Từ (1) và (2)
\(\Rightarrow\frac{a}{12}=\frac{b}{21}=\frac{c}{35}=\frac{2a}{24}=\frac{2a-b+c}{24-21+35}=\frac{114}{38}=3\)
\(\Rightarrow\hept{\begin{cases}a=3.12=36\\b=3.21=63\\c=3.35=105\end{cases}}\)
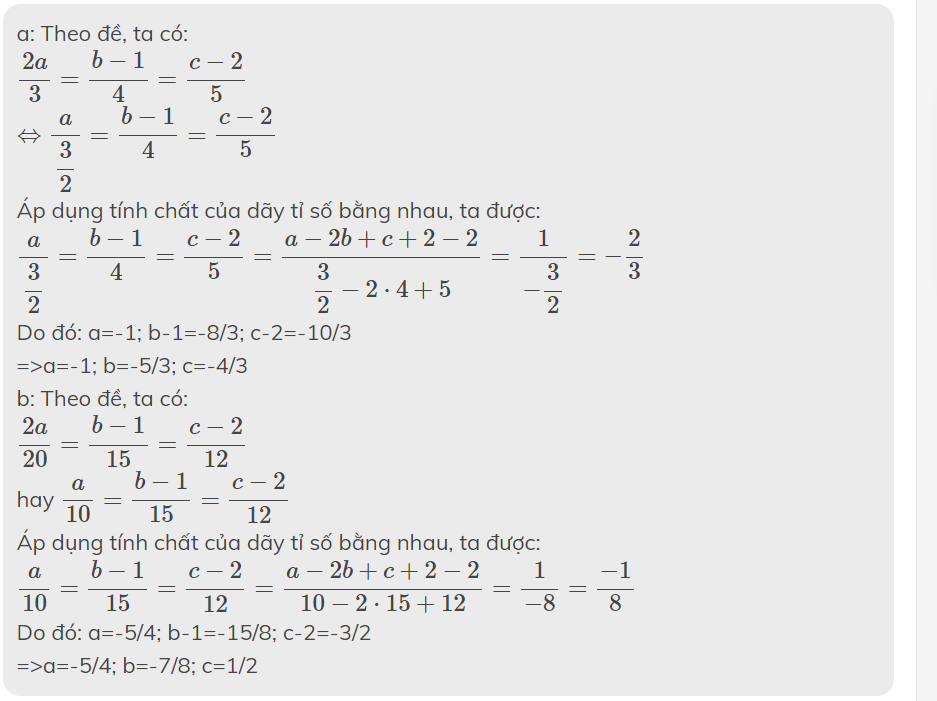
giúp mình nhé
\(a,\Leftrightarrow\left\{{}\begin{matrix}a=b+1\\2b+2+b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1+1=2\\b=1\end{matrix}\right.\\ b,\Leftrightarrow\left\{{}\begin{matrix}2a-4+a=7\\b=4-a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{11}{3}\\b=4-\dfrac{11}{3}=\dfrac{1}{3}\end{matrix}\right.\)