K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DN
1
HP
10 tháng 2 2017
x2+x+1=x2+2x+1-x-1+1=(x+1)2-(x+1)+1
x2+2x+1=(x+1)2
đặt x+1=y , A=(y2-y+1)/y2=1-1/y+1/y2
tiếp tục đặt 1/y=z ta đc A=z2-z+1=(z-1/2)2+3/4 >= 3/4
minA=3/4 dấu "=" khi z=1/2<=>y=2<=>x=1
H
0
TT
0
TN
1
9 tháng 11 2021
\(P=\left(x+1\right)\left(x-6\right)\left(x-2\right)\left(x-3\right)-36\)
\(P=\left(x^2-6x+x-6\right)\left(x^2-3x-2x+6\right)-36\)
\(P=\left(x^2-5x-6\right)\left(x^2-5x+6\right)-36\)
\(P=\left(x^2-5x\right)^2-6^2-36\)
\(P=\left(x^2-5x\right)^2-72\)
Vì \(\left(x^2-5x\right)^2\ge0\Leftrightarrow\left(x^2-5x\right)^2-72\ge-72\Leftrightarrow P\ge-72\Leftrightarrow min_P=-72\)
Đẳng thức xảy ra \(\Leftrightarrow x^2-5x=0\Leftrightarrow x\left(x-5\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=5\end{cases}}\)
Vậy GTNN của P là -72 khi x = 0 hoặc x = 5
NP
1
5 tháng 6 2016
Để E > 1
Thì \(\frac{x^2}{x-1}\)>1
<==>\(x-1\)>0
<==>x > 1
Vậy x > 1 thì E > 1
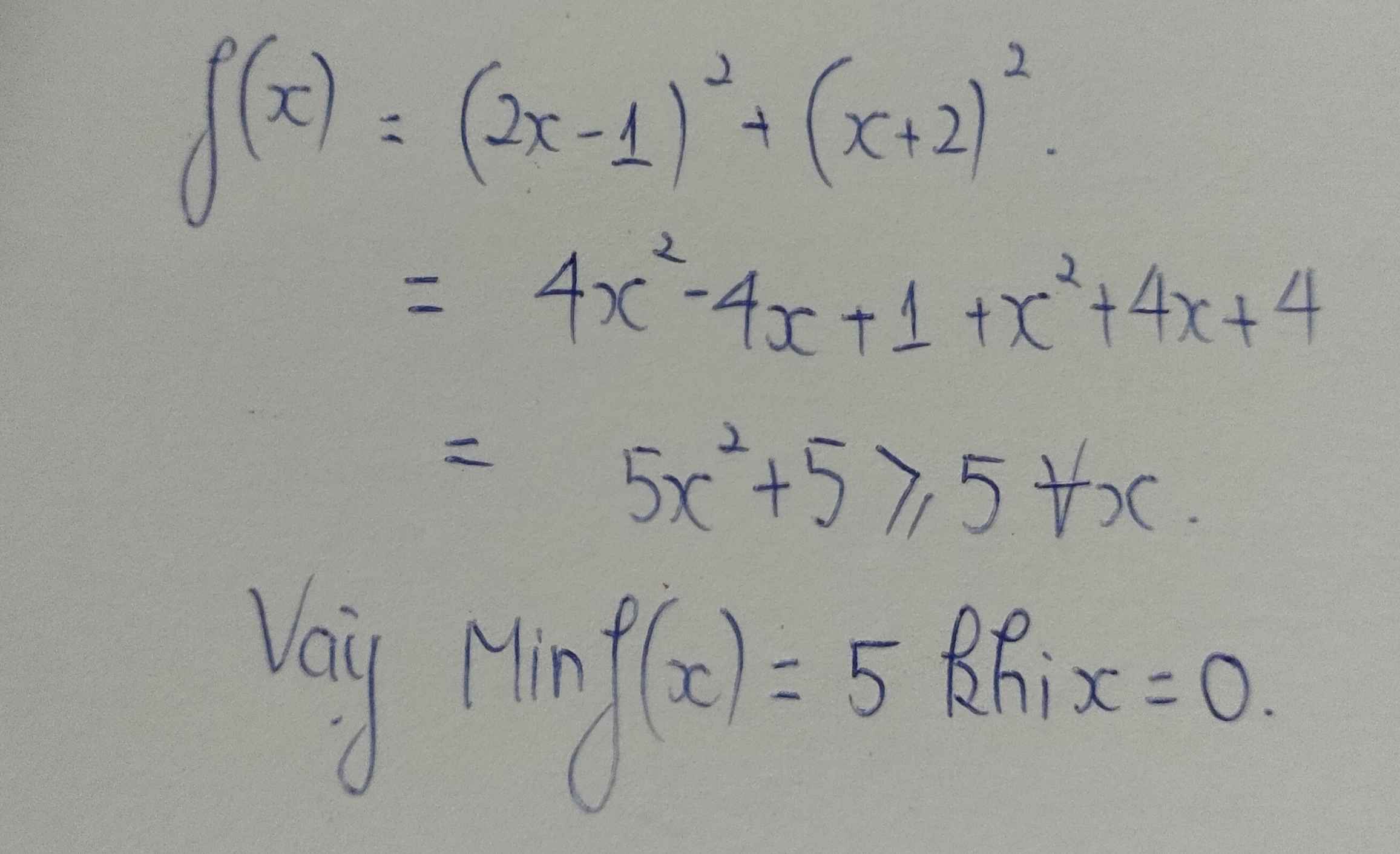
\(Q=x^2+x+\dfrac{1}{4}+\dfrac{3}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ Q_{min}=\dfrac{3}{4}\Leftrightarrow x=-\dfrac{1}{2}\)
Q=(x+1)2
GTNN là Q=0
xảy ra khi (x+1)2=0
x+1=0
x =-1