Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Bài 1:
Ta nhớ công thức \(\sin^2x=\frac{1-\cos 2x}{2}\). Áp dụng vào bài toán:
\(F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx\)
\(\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})\)
\(\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c\)
Giải thích 1 chút: \(d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx\)
Vì \(F(0)=8\Rightarrow -1+c=8\Rightarrow c=9\)
\(\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9\)
Câu 2:
Áp dụng nguyên hàm từng phần như bài bạn đã đăng:
\(\Rightarrow F(x)=-xe^{-x}-e^{-x}+c\)
Vì \(F(0)=1\Rightarrow -1+c=1\Rightarrow c=2\)
\(\Rightarrow F(x)=-e^{-x}(x+1)+2\), tức B là đáp án đúng

Dãy số 123456678787667677777676544789879876986.... lớn hơn.
Số lớn nhất ở dãy tổng có 14 chữ số << vế phải có hơn 50 số.(theo bản năng cảm nhận thấy thế)
Mình nghĩ bài này muốn làm chắc chắn thì chỉ có cách cộng từng hàng đơn vị, hàng chục, hàng trăm,..... r so sánh với hàng đơn vị,hàng chục hàng trăm,....của vế phải thoiiiiiiiiiiiii.
9+6+0+0+9+7+1+0+8+8+3+1+0+9+7+0+0+1+9+1+2+8+8+8+7+7+3+6+2+8+3+0+3+8+4+7+5+8=180 => hàng đơn vị =0 nhớ 18.
18+8+5+8+9+8+8+2+7+9+8+4+2+9+2+8+9+9+2+8+2+3+0+8+7+7+6+4+7+3+7+2+9+5+8+4+2+5+8=240 => hàng chục=0 nhớ 24
24+7+4+6++8+7+9+3+8+0+9+4+3+8+4+9+8+8+3+7+3+4+9+7+..........................................................................................
..................................................................................................................................................................................................
Còn cao nhân nào có cách khác hay k chỉ giáo với...
Giải giúp mình chi tiết câu này với ạ 🙏🏻🙏🏻
1, Cho tam diện OABC vuông tại O. Biết tam giác ABC đều cạnh #Hỏi cộng đồng OLM #Toán lớp 12


Do \(x;y\in\left[0;2\right]\Rightarrow\left\{{}\begin{matrix}x\left(2-x\right)\ge0\\y\left(2-y\right)\ge0\end{matrix}\right.\) \(\Rightarrow2x^2+4y^2\le4x+8y\)
\(P\le3^0+5^0+3^z+4\left(x+2y\right)=2+3^z+4\left(6-z\right)=3^z-4z+26\)
Xét hàm \(f\left(z\right)=3^z-4z+26\) trên \(\left[0;2\right]\)
\(f'\left(z\right)=3^z.ln3-4=0\Rightarrow z=log_3\left(\dfrac{4}{ln3}\right)=a\)
\(f\left(0\right)=27\) ; \(f\left(2\right)=27\); \(f\left(a\right)\approx-1,1\)
\(\Rightarrow f\left(z\right)\le27\Rightarrow maxP=27\)
(Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(0;2;2\right)\))
Ồ mà khoan, bài trước bị nhầm lẫn ở chỗ \(3^{2x-x^2}+5^{2y-y^2}\ge3^0+5^0\) mới đúng, ko để ý bị ngược dấu đoạn này
Vậy giải cách khác:
\(0\le x;y;z\le2\Rightarrow x\left(2-x\right)\ge0\Rightarrow2x-x^2\ge0\)
Lại có: \(2x-x^2=1-\left(x-1\right)^2\le1\)
\(\Rightarrow0\le2x-x^2\le1\)
Tương tự ta có: \(0\le2y-y^2\le1\)
Xét hàm: \(f\left(t\right)=3^t-2t\) trên \(\left[0;1\right]\)
\(f'\left(t\right)=3^t.ln3-2=0\Rightarrow t=log_3\left(\dfrac{2}{ln3}\right)=a\)
\(f\left(0\right)=1;\) \(f\left(1\right)=1\) ; \(f\left(a\right)\approx0,73\)
\(\Rightarrow f\left(t\right)\le1\Rightarrow3^t-2t\le1\Rightarrow3^t\le2t+1\)
\(\Rightarrow3^{2x-x^2}\le2\left(2x-x^2\right)+1\)
Hoàn toàn tương tự, ta chứng minh được:
\(5^t\le4t+1\) với \(t\in\left[0;1\right]\Rightarrow5^{2y-y^2}\le4\left(2y-y^2\right)+1\)
\(3^t\le4t+1\) với \(t\in\left[0;2\right]\Rightarrow3^z\le4z+1\)
\(\Rightarrow P\le2\left(2x-x^2\right)+4\left(2y-y^2\right)+4z+3+2x^2+4y^2=4\left(x+2y+z\right)+3=27\)
Lần này thì ko sai được rồi

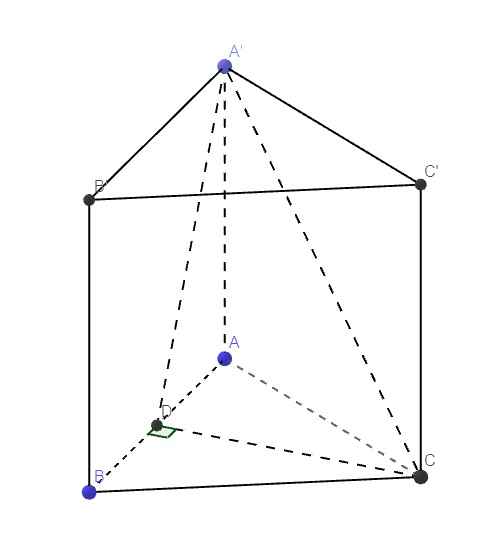
Gọi D là trung điểm AB \(\Rightarrow CD\perp AB\)
\(\Rightarrow CD\perp\left(AA'B'B\right)\)
\(\Rightarrow\widehat{CA'D}=30^0\)
\(CD=\dfrac{a\sqrt{3}}{2}\Rightarrow A'D=\dfrac{CD}{tan30^0}=\dfrac{3a}{2}\)
\(\Rightarrow A'A=\sqrt{CD^2-AD^2}=a\sqrt{2}\)
\(V=\dfrac{1}{3}A'A.S_{ABC}=\dfrac{1}{3}.a\sqrt{2}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{6}}{12}\)


\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=1\\x=1\Rightarrow y=0\\x=-1\Rightarrow y=0\end{matrix}\right.\)
\(\Rightarrow A\left(0;1\right);B\left(1;0\right);C\left(-1;0\right)\)
\(S=\dfrac{1}{2}.\left|y_A-y_B\right|.\left|x_B-x_C\right|=\dfrac{1}{2}.1.2=1\)