
GIẢI MÃ KỲ THI ĐÁNH GIÁ NĂNG LỰC HSA - ĐHQGHN ĐỂ NHẬN THƯỞNG CÙNG HOC24!!!
Thời gian gần đây, các bạn học sinh rất quan tâm tới kỳ thi đánh giá năng lực. Vì vậy, HOC24 đã tổ chức cuộc thi "Giải mã kỳ thi đánh giá năng lực HSA - ĐHQGHN".
- Mục đích: Tạo ra không gian để các bạn học sinh nêu những chia sẻ, những đánh giá khách quan và thiết thực về kỳ thi đánh giá năng lực HSA của Đại học quốc gia Hà Nội – ngày 10/3, đồng thời tìm được HSA REVIEWER xứng đáng.
- Ý nghĩa: Cung cấp những thông tin hữu ích về đề thi HSA – ĐGQGHN cho những bạn có ôn thi ĐGNL hoặc có nhu cầu tìm hiểu về kỳ thi đánh giá năng lực HSA.
- Đối tượng: Các thí sinh đã tham dự kỳ thi HSA – ĐHQGHN đợt 301.
- Quy định: Viết một bài chia sẻ về kỳ thi ĐGNL HSA (đợt 301 – ngày 10/3/2023) với nội dung chính là review đề thi: (1) mức độ khó so với đề mẫu, (2) nhận xét từng phần thi (Tư duy định tính, tư duy định lượng, khoa học), (3) Tỉ lệ theo mức độ câu hỏi; phân bổ kiến thức ở các khối lớp 10 - 11- 12; (4) nội dung câu hỏi (nhớ càng nhiều càng tốt, nhớ ý chứ ko cần chính xác), bài đọc lấy ở đâu, câu hỏi thuộc thể loại nào; (5) Bạn ấn tượng nhất về câu hỏi nào và tại sao; v.v.
Ngoài ra, bạn có thể viết bài chia sẻ kinh nghiệm thi:
+ Những kinh nghiệm khi bước vào phòng thi ĐGNL HAS (đồ dùng được mang vào, thủ tục, ...)
+ Kinh nghiệm khi thi: Thao tác với máy tính, tinh thần làm bài, ...
+ Lời khuyên cho các kỳ thi HAS- ĐHQGHN sắp tới: Ôn tập kiến thức, tinh thần, sức khỏe, luyện tập kĩ năng làm bài trên máy tính, ...
- Đánh giá và giải thưởng:
BTC sẽ dựa trên số like cũng như đánh giá của các thầy cô giáo HOC24 để trao giải.
Giải thưởng gồm:
+ 1-3 giải nhất: 200 000 đồng
+ 5-10 giải nhì: 100 000 đồng
+ 10 - 20 giải ba: 50 coin
- Thời gian: Cuộc thi diễn ra từ 14/3/2023 đến hết ngày 16/3/2023. Giải thưởng được công bố vào ngày 18/3/2023.
Chúc các bạn có các bài chia sẻ thật hay và dành được phần thưởng của hoc24!









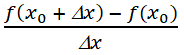
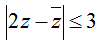
kẻ mỗi cái bảng biến thiên ra rồi xét là xog
\(y'=4x^3+4x=0\) \(\Leftrightarrow\)\(x=0\)
\(f\left(-1\right)=2\)
\(f\left(0\right)=-1\)
\(f\left(2\right)=23\)
=> MAX y trên [-1; 2] = 23