Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1:
\(\dfrac{BC}{sin\widehat{A}}=\dfrac{AB}{sin\widehat{C}}=\dfrac{AC}{sin\widehat{B}}\)
Ta có \(\widehat{C}=\widehat{B}\) ( tam giác ABC cân tại A )
\(\widehat{B}+\widehat{C}=180^0-\widehat{A}\) \(\Leftrightarrow2\widehat{B}=180^0-\widehat{A}\Leftrightarrow\widehat{B}=90^0-\dfrac{\widehat{A}}{2}\)
\(\Rightarrow sin\widehat{B}=sin\left(90^0-\dfrac{\widehat{A}}{2}\right)=cos\left(\dfrac{\widehat{A}}{2}\right)\)
\(\Rightarrow\dfrac{BC}{sin\widehat{A}}=\dfrac{AC}{cos\left(\dfrac{\widehat{A}}{2}\right)}\) \(\Leftrightarrow\sqrt{3}.cos\left(\dfrac{\widehat{A}}{2}\right)=2.sin\left(\dfrac{\widehat{A}}{2}\right).cos\left(\dfrac{\widehat{A}}{2}\right)\)
( tam giác ABC có \(\widehat{A}\ne180^0\Rightarrow\dfrac{\widehat{A}}{2}\ne90^0\Rightarrow cos\left(\dfrac{\widehat{A}}{2}\right)\ne0\) )
\(\Rightarrow\sqrt{3}=2sin\left(\dfrac{\widehat{A}}{2}\right)\) \(\Leftrightarrow\dfrac{\widehat{A}}{2}=60^0\Leftrightarrow\widehat{A}=120^0\)
Vậy độ mở của màn hình máy tính là \(120^0\)
Cách 2: Do AB=AC nên tam giác ABC cân tại A
Kẻ \(AH\perp BC\) tại H
Tam giác ABC cân tại A có AH vừa là đường cao, vừa là đường phân giác, vừa là đường trung tuyến
\(\Rightarrow\)H là trung điểm của BC \(\Rightarrow BH=\dfrac{BC}{2}=15\sqrt{3}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông có:
\(sin\widehat{BAH}=\dfrac{BH}{AB}=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{BAH}=60^0\)
\(\Rightarrow\widehat{BAC}=2\widehat{BAH}=120^0\)
Vậy độ mở của màn hình máy tính là \(120^0\)


Ảnh của A, B, C lần lượt là trung điểm A', B', C' của các cạnh HA, HB, HC.

Ảnh của A, B, C lần lượt là trung điểm A', B', C' của các cạnh HA, HB, HC.

Giả sử 3 cạnh của tam giác ABC theo thứ tự a, b, c. Không giảm tính tổng quát, ta giả sử 0 < a \(\le b\le c\), nếu chúng tạo thành cấp số nhân thì, theo tính chất của cấp số nhân ta có : \(b^2=ac\)
Theo định lí hàm số côsin, ta có :
\(b^2=a^2+c^2-2ac\cos B\Rightarrow ac=a^2+c^2-2ac.\cos B\)
\(\Leftrightarrow\cos B=\frac{a^2+c^2}{2ac}-\frac{1}{2}\)
Mặt khác \(a^2+c^2\ge2ac\Rightarrow\cos B\ge1-\frac{1}{2}=\frac{1}{2}\)
Vậy góc \(B\le60^0\)
Nhưng \(a\le b\Rightarrow A\le60^0\) cho nên tam giác ABC có 2 góc không quá \(60^0\)

Do \(d\perp\left(ABC\right)\) nên \(MN\perp BC\)
\(\left\{{}\begin{matrix}MC\perp\left(BOH\right)\\BN\subset\left(BOH\right)\end{matrix}\right.\) \(\Rightarrow MC\perp BN\)
\(\left\{{}\begin{matrix}MB\perp\left(CHO\right)\\CN\subset\left(CHO\right)\end{matrix}\right.\)\(\Rightarrow MB\perp CN\)

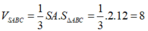
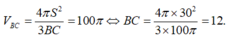

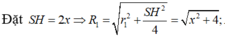
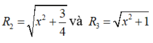


Giả sử AB=9a ⇒ BC=10a ; AC=17a
⇒p=(9a+10a+17a)/2=18a
Sử dụng hệ thức heron ta có:
144^2=18a(18a−9a)(18a−10a)(18a−17a)=1296a^4
⇔a=2a=2 (cm)
Vậy 3 cạnh tam giác có độ dài là: 18 cm; 20 cm; 34 cm