Tìm đạo hàm của các hàm số sau y = sin...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

27 tháng 3 2017

Tìm đạo hàm của các hàm số sau y = sin x x + x sin x

#Hỏi cộng đồng OLM #Toán lớp 11

1

CM

Cao Minh Tâm

27 tháng 3 2017

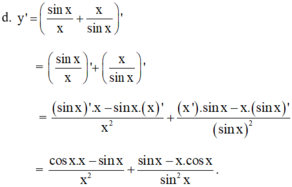
Bài 3 trang 169 sgk Đại Số 11 | Để học tốt Toán 11

Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG

Sách Giáo Khoa

4 tháng 4 2017

Tìm đạo hàm của các hàm số sau :

a) \(y=5\sin x-3\cos x\)

b) \(y=\dfrac{\sin x+\cos x}{\sin x-\cos x}\)

c) \(y=x\cos x\)

d) \(y=\dfrac{\sin x}{x}+\dfrac{x}{\sin x}\)

e) \(y=\sqrt{1+2\tan x}\)

f) \(y=\sin\sqrt{1+x^2}\)

#Hỏi cộng đồng OLM #Toán lớp 11

1

MH

Minh Hải

9 tháng 4 2017

a) y' = 5cosx -3(-sinx) = 5cosx + 3sinx;

b) $y'=\frac{(sinx+cos x)'.(sin x- cos x)-(sin x+cos x)(sin x-cos x)'}{(sin x-cos x)^{2}}$ = $\frac{(cos x-sin x)(sin x -cos x)-(sin x+ cos x)(cosx+sinx)}{(sin x-cosx )^{2}}$ = $\frac{-2}{(sin x-cos x)^{2}}$ .

c) y' = cotx +x. $\left ( -\frac{1}{sin^{2}x} \right )$ = cotx - $\frac{x}{sin^{2}x}$ .

d) $y'=\frac{(sin x)'.x-sin x.(x)'}{x^{2}}$ + $\frac{(x)'.sin x-x(sin x)'}{sin^{2}x}$ = $\frac{x.cosx-sinx}{x^{2}}+\frac{sin x-x.cosx}{sin^{2}x}$ = (x. cosx -sinx) $\left ( \frac{1}{x^{2}}-\frac{1}{sin^{2}x} \right )$ .

e) $y'=\frac{(1+2tanx)'}{2\sqrt{1+2tanx}}$ = $\frac{\frac{2}{cos^{2}x}}{2\sqrt{1+2tanx}}$ = $\frac{1}{cos^{2}x\sqrt{1+2tanx}}$ .

f) y' = (√(1+x²))' cos√(1+x²) = $\frac{(1+x^{2})'}{2\sqrt{1+x^{2}}}$ cos√(1+x²) = $\frac{x}{\sqrt{1+x^{2}}}$ cos√(1+x²).

SG

Sách Giáo Khoa

11 tháng 4 2017

Tìm đạo hàm của hàm số sau :

\(y=\dfrac{\sin x-x\cos x}{\cos x+x\sin x}\)

#Hỏi cộng đồng OLM #Toán lớp 11

1

NT

nguyen thu phuong

27 tháng 3 2020

SG

Sách Giáo Khoa

4 tháng 4 2017

Tìm đạo hàm của các hàm số sau : a) \(y=2\sqrt{x}\sin x-\dfrac{\cos x}{x}\) b) \(y=\dfrac{3\cos x}{2x+1}\) c) \(y=\dfrac{t^2+2\cos t}{\sin t}\) d) \(y=\dfrac{2\cos\varphi-\sin\varphi}{3\sin\varphi+\cos\varphi}\) e) \(y=\dfrac{\tan x}{\sin x+2}\) f) \(y=\dfrac{\cot...

#Hỏi cộng đồng OLM #Toán lớp 11

1

QD

Quang Duy

4 tháng 4 2017

Giải bài 2 trang 176 sgk Đại Số 11 | Để học tốt Toán 11

Giải bài 2 trang 176 sgk Đại Số 11 | Để học tốt Toán 11

Giải bài 2 trang 176 sgk Đại Số 11 | Để học tốt Toán 11

SG

Sách Giáo Khoa

11 tháng 4 2017

Tìm đạo hàm của hàm số sau :

\(y=\left(x\sin\alpha+\cos\alpha\right)\left(x\cos\alpha-\sin\alpha\right)\)

#Hỏi cộng đồng OLM #Toán lớp 11

0

SG

Sách Giáo Khoa

11 tháng 4 2017

Tìm đạo hàm của hàm số sau :

\(y=\left(2-x^2\right)\cos x+2x\sin x\)

#Hỏi cộng đồng OLM #Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 5 2022

Tham khảo:

SG

Sách Giáo Khoa

11 tháng 4 2017

Tìm đạo hàm cấp hai của hàm số sau :

\(y=x^2\sin x\)

#Hỏi cộng đồng OLM #Toán lớp 11

1

P

phamthiphuong

8 tháng 5 2017

\(y'\left(x\right)=\left(x^2\right)'sinx+x^2.\left(sinx\right)'\)\(=2x.sinx+x^2.cosx\)
\(y''\left(x\right)=\left[2x.sinx+x^2.cosx\right]'\)\(=\left(2xsinx\right)'\)\(+\left(x^2.cosx\right)'\)
\(=2sinx+2xcosx+2x.cosx+x^2.\left(-sinx\right)\)\(=2sinx+4x.cosx-x^2sinx\).

B

Buddy

17 tháng 8 2023

Tính đạo hàm của các hàm số sau:

a) \(y = x{\sin ^2}x;\)

b) \(y = {\cos ^2}x + \sin 2x;\)

c) \(y = \sin 3x - 3\sin x;\)

d) \(y = \tan x + \cot x.\)

#Hỏi cộng đồng OLM #Toán lớp 11

1

BN

Bùi Nguyên Khải

17 tháng 8 2023

tham khảo:

a)\(y'=xsin2x+sin^2x\)

\(y'=sin^2x+xsin2x\)

b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)

c)\(y=sin3x-3sinx\)

\(y'=3cos3x-3cosx\)

d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)

\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)

BT

Bình Trần Thị

31 tháng 8 2016

từ đồ thị hàm số y = \(\sin x\) , hãy suy ra đồ thị các hàm số sau và vẽ các đồ thị các hàm số đó : a) y = \(-\sin x\) ; b) y = \(\left|\sin x\right|\) ; c) y = \(\sin\left|x\right|\)

#Hỏi cộng đồng OLM #Toán lớp 11

0

BT

Bình Trần Thị

4 tháng 9 2016

từ đồ thị hàm số y = \(\sin x\) , hãy suy ra đồ thị các hàm số sau và vẽ các đồ thị các hàm số đó : a) y = \(-\sin x\) ; b) y = \(\left|\sin x\right|\) ; c) y = \(\sin\left|x\right|\)

#Hỏi cộng đồng OLM #Toán lớp 11

0

BT

Bình Trần Thị

2 tháng 9 2016

từ đồ thị hàm số y = \(\sin x\) , hãy suy ra đồ thị các hàm số sau và vẽ các đồ thị các hàm số đó : a) y = \(-\sin x\) ; b) y = \(\left|\sin x\right|\) ; c) y = \(\sin\left|x\right|\)

#Hỏi cộng đồng OLM #Toán lớp 11

0