Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
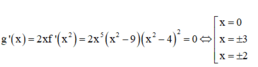
Bảng biến thiên của hàm số y= g( x)
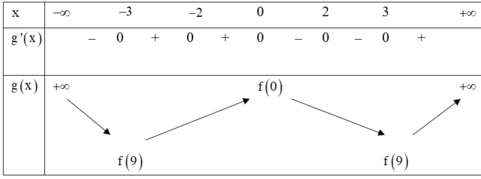
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞) hàm số nghịch biến trong khoảng (-∞; -3) .
Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3
Vậy có 3 khẳng định đúng là khẳng định I, II, IV
Chọn C.
Tìm cực trị của các hàm số sau:

Vì x 2 – 2x + 5 luôn luôn dương nên hàm số xác định trên (− ∞ ; + ∞ )
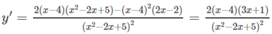
y′ = 0 ⇔ 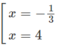
Bảng biến thiên:
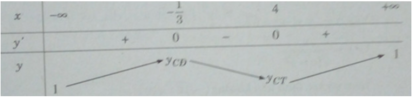
Hàm số đạt cực đại tại x = −1/3, đạt cực tiểu tại x = 4 và y CD = y(−1/3) = 13/4; y CT = y(4) = 0

Xét trên các miền xác định của các hàm (bạn tự tìm miền xác định)
a.
\(y'=\dfrac{1}{2\sqrt{x-3}}-\dfrac{1}{2\sqrt{6-x}}=\dfrac{\sqrt{6-x}-\sqrt{x-3}}{2\sqrt{\left(x-3\right)\left(6-x\right)}}\)
\(y'=0\Rightarrow6-x=x-3\Rightarrow x=\dfrac{9}{2}\)
\(x=\dfrac{9}{2}\) là điểm cực đại của hàm số
b.
\(y'=1-\dfrac{9}{\left(x-2\right)^2}=0\Rightarrow\left(x-2\right)^2=9\Rightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
\(x=-1\) là điểm cực đại, \(x=5\) là điểm cực tiểu
c.
\(y'=\sqrt{3-x}-\dfrac{x}{2\sqrt{3-x}}=0\Rightarrow2\left(3-x\right)-x=0\)
\(\Rightarrow x=2\)
\(x=2\) là điểm cực đại
d.
\(y'=\dfrac{-x^2+4}{\left(x^2+4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
\(x=-2\) là điểm cực tiểu, \(x=2\) là điểm cực đại
e.
\(y'=\dfrac{-8\left(x^2-5x+4\right)}{\left(x^2-4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
\(x=1\) là điểm cực tiểu, \(x=4\) là điểm cực đại
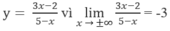




\(\left\{{}\begin{matrix}z'_x=-2x.e^{y-x^2+5}+8x^3=0\\z'_y=e^{y-x^2+5}-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\left(8x^2-2e^{y-x^2+5}\right)=0\\y-x^2+5=0\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x=0\\y-x^2+5=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=-5\end{matrix}\right.\)
Th2: \(\left\{{}\begin{matrix}4x^2=e^{y-x^2+5}\\y-x^2+5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x^2=1\\y-x^2+5=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\frac{1}{2}\\y=-\frac{19}{4}\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}x=-\frac{1}{2}\\y=-\frac{19}{4}\end{matrix}\right.\)
Ta có các điểm dừng: \(M\left(0;-5\right)\) ; \(N\left(\frac{1}{2};-\frac{19}{4}\right)\) ; \(P\left(-\frac{1}{2};-\frac{19}{4}\right)\)
\(z''_{xx}=\left(4x^2-2\right)e^{y-x^2+5}+24x^2\)
\(z''_{xy}=-2x.e^{y-x^2+5}\) ; \(z''_{yy}=e^{y-x^2+5}\)
Tại M: \(A=-2\) ; \(B=0\) ; \(C=1\Rightarrow B^2-AC=2>0\Rightarrow M\) không phải cực trị
Tại N: \(A=5>0\) ; \(B=-1\) ; \(C=1\Rightarrow B^2-AC=-4< 0\Rightarrow\) hàm đạt cực tiểu tại N
Tại P: \(A=5>0\) ; \(B=1\) ; \(C=1\Rightarrow B^2-AC=-4< 0\Rightarrow\) hàm đạt cực tiểu tại P
Cảm ơn b