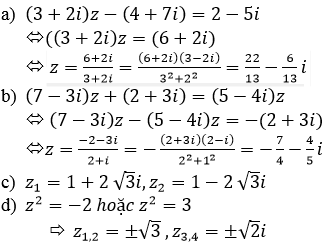Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1)
Gọi số phức $z$ có dạng \(z=a+bi(a,b\in\mathbb{R})\).
Ta có \(|z|+z=3+4i\Leftrightarrow \sqrt{a^2+b^2}+a+bi=3+4i\)
\(\Rightarrow\left\{\begin{matrix}\sqrt{a^2+b^2}+a=3\\b=4\end{matrix}\right.\Rightarrow\left\{\begin{matrix}a=\frac{5}{6}\\b=4\end{matrix}\right.\)
Vậy số phức cần tìm là \(\frac{5}{6}+4i\)
b)
\(\left\{\begin{matrix} z_1+3z_1z_2=(-1+i)z_2\\ 2z_1-z_2=3+2i\end{matrix}\right.\Rightarrow \left\{\begin{matrix} \frac{z_1}{z_2}+3z_1=-1+i\\ 2z_1-z_2=3+2i\end{matrix}\right.\Rightarrow \frac{z_1}{z_2}+z_1+z_2=(-1+i)-(3+2i)=-4-i\)
\(\Leftrightarrow w=-4-i\Rightarrow |w|=\sqrt{17}\)

Câu 1:
Gọi \(A\left(1;-1\right)\) và \(B\left(2;3\right)\Rightarrow\) tập hợp \(z\) thoả mãn điều kiện đề bài là đường trung trực d của đoạn AB, ta dễ dàng viết được phương trình d có dạng \(4x-y-5=0\)
Gọi \(M\left(-2;-1\right)\) và \(N\left(3;-2\right)\) và \(I\left(a;b\right)\) là điểm bất kì biểu diễn \(z\Rightarrow I\in d\) \(\Rightarrow P=IM+IN\). Bài toán trở thành dạng cực trị hình học phẳng quen thuộc: cho đường thẳng d và 2 điểm M, N cố định, tìm I thuộc d để \(P=IM+IN\) đạt GTNN
Thay toạ độ M, N vào pt d ta được 2 giá trị trái dấu \(\Rightarrow M;N\) nằm về 2 phía so với d
Gọi \(C\) là điểm đối xứng M qua d \(\Rightarrow IM+IN=IC+IN\), mà \(IC+IN\ge CN\Rightarrow P_{min}=CN\) khi I, C, N thẳng hàng
Phương trình đường thẳng d' qua M và vuông góc d có dạng:
\(1\left(x+2\right)+4\left(y+1\right)=0\Leftrightarrow x+4y+6=0\)
Gọi D là giao điểm d và d' \(\Rightarrow\left\{{}\begin{matrix}x+4y+6=0\\4x-y-5=0\end{matrix}\right.\) \(\Rightarrow D\left(\frac{14}{17};-\frac{29}{17}\right)\)
\(\overrightarrow{MD}=\overrightarrow{DC}\Rightarrow C\left(-2;-1\right)\Rightarrow P_{min}=CN=\sqrt{\left(3+2\right)^2+\left(-2+1\right)^2}=\sqrt{26}\)
Bài 2:
Tập hợp \(z\) là các điểm M thuộc đường tròn (C) tâm \(I\left(0;1\right)\) bán kính \(R=\sqrt{2}\) có phương trình \(x^2+\left(y-1\right)^2=2\)
\(\Rightarrow\left|z\right|=OM\Rightarrow\left|z\right|_{max}\) khi và chỉ khi \(M;I;O\) thẳng hàng và M, O nằm về hai phía so với I
\(\Rightarrow M\) là giao điểm của (C) với Oy \(\Rightarrow M\left(0;1+\sqrt{2}\right)\Rightarrow\) phần ảo của z là \(b=1+\sqrt{2}\)
Câu 3:
\(\overline{z}=\left(i+\sqrt{2}\right)^2\left(1-\sqrt{2}i\right)=5+\sqrt{2}i\)
\(\Rightarrow z=5-\sqrt{2}i\Rightarrow b=-\sqrt{2}\)
Câu 4
\(z.z'=\left(m+3i\right)\left(2-\left(m+1\right)i\right)=2m-\left(m^2+m\right)i+6i+3m+3\)
\(=5m+3-\left(m^2+m-6\right)i\)
Để \(z.z'\) là số thực \(\Leftrightarrow m^2+m-6=0\Rightarrow\left[{}\begin{matrix}m=2\\m=-3\end{matrix}\right.\)
Câu 5:
\(A\left(-4;0\right);B\left(0;4\right);M\left(x;3\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(4;4\right)\\\overrightarrow{AM}=\left(x+4;3\right)\end{matrix}\right.\) \(\Rightarrow A,B,M\) khi và chỉ khi \(\frac{x+4}{4}=\frac{3}{4}\Rightarrow x=-1\)
Câu 6:
\(z=3z_1-2z_2=3\left(1+2i\right)-2\left(2-3i\right)=-1+12i\)
\(\Rightarrow b=12\)
Câu 7:
\(w=\left(1-i\right)^2z\)
Lấy môđun 2 vế:
\(\left|w\right|=\left|\left(1-i\right)^2\right|.\left|z\right|=2m\)
Câu 8:
\(3=\left|z-1+3i\right|=\left|z-1-i+4i\right|\ge\left|\left|z-1-i\right|-\left|4i\right|\right|=\left|\left|z-1-i\right|-4\right|\)
\(\Rightarrow\left|z-1-i\right|\ge-3+4=1\)

Giải:
Đặt \(z=a+bi(a,b\in\mathbb{R})\)
Theo bài ra ta có: \(z-(2+3i)\overline{z}=1-9i\)
\(\Leftrightarrow (a+bi)-(2+3i)(a-bi)=1-9i\)
\(\Leftrightarrow -(a+3b)+3i(b-a)=1-9i\)
\(\left\{\begin{matrix} a+3b=-1\\ b-a=-3\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=2\\ b=-1\end{matrix}\right.\Rightarrow z=2-i\)

a) (3 + 2i)z – (4 + 7i) = 2 – 5i
⇔(3+2i)z=6+2i
<=> z = \(\dfrac{\text{6 + 2 i}}{\text{3 + 2 i}}\) = \(\dfrac{22}{13}\) - \(\dfrac{6}{13}\)i
b) (7 – 3i)z + (2 + 3i) = (5 – 4i)z
⇔(7−3i−5+4i)=−2−3i
⇔z= \(\dfrac{\text{− 2 − 3 i}}{\text{2 + i}}\) = \(\dfrac{-7}{5}\) - \(\dfrac{4}{5}i\)
c) z2 – 2z + 13 = 0
⇔ (z – 1)2 = -12 ⇔ z = 1 ± 2 √3 i
d) z4 – z2 – 6 = 0
⇔ (z2 – 3)(z2 + 2) = 0
⇔ z ∈ { √3, - √3, √2i, - √2i}

Giải:
Đặt \(z=a+bi(a,b\in\mathbb{R})\)
Theo bài ra ta có:
\(\left\{\begin{matrix} |(a-2)+i(b-1)|=\sqrt{10}\\ z\overline{z}=|z|^2=a^2+b^2=25\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (a-2)^2+(b-1)^2=10\\ a^2+b^2=25\end{matrix}\right.\)
\(\left\{\begin{matrix} 2a+b=10\\ a^2+b^2=25\end{matrix}\right.\Rightarrow a^2+(10-2a)^2=25\rightarrow a=5\) hoặc \(a=3\)
\(\Rightarrow b=0;4\)
Vậy \(z\in \left \{5,3+4i\right\}\)

đặc \(z=a+bi\) với \(\left(a;b\in R;i^2=-1\right)\)
ta có : \(\left|z-\overline{z}+2i\right|=\left|\dfrac{3}{2}z+\dfrac{1}{2}\overline{z}\right|\)
\(\Leftrightarrow\left|a+bi-a+bi+2i\right|=\left|\dfrac{3}{2}a+\dfrac{3}{2}bi+\dfrac{1}{2}a-\dfrac{1}{2}bi\right|\)
\(\Leftrightarrow\sqrt{\left(2b+2\right)^2}=\sqrt{\left(2a+b\right)^2}\) \(\Leftrightarrow2b+2=2a+b\Leftrightarrow a=\dfrac{b}{2}+1\)
ta có : \(P=\left|z-3\right|=\left|a+bi-3\right|=\sqrt{\left(a-3\right)^2+b^2}\)
\(\Leftrightarrow P=\sqrt{\left(\dfrac{b}{2}+1-3\right)^2+b^2}=\sqrt{\left(\dfrac{b}{2}-2\right)^2+b^2}\)
\(\Leftrightarrow P=\sqrt{\dfrac{5b^2}{4}-2b+4}\ge\sqrt{4-\dfrac{\left(-2\right)^2}{4.\dfrac{5}{4}}}=\dfrac{4\sqrt{5}}{5}\)
dấu "=" xảy ra khi \(b=\dfrac{2}{2.\dfrac{5}{4}}=\dfrac{4}{5}\) và \(a=\dfrac{7}{5}\) \(\Leftrightarrow z=\dfrac{7}{5}+\dfrac{4}{5}i\)