Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
bài 1
coi bậc 2 với ẩn x tham số y D(x) phải chính phường
<=> (2y-3)^2 -4(2y^2 -3y+2) =k^2
=> -8y^2 +1 =k^2 => y =0
với y =0 => x =-1 và -2
a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
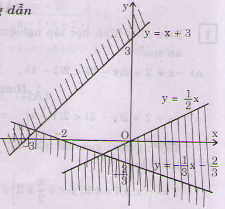
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
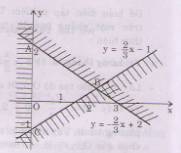
Ta có: điều kiện xác định của bpt \(x+3-\dfrac{1}{x+7}< -\dfrac{1}{x+7}\) là \(x\ne-7\)
\(\Rightarrow x=-7\) không phải là nghiệm của bpt trên
Lại có: \(x+3< 2\\ \Leftrightarrow x< 2-3\\ \Leftrightarrow x< -1\)
\(\Rightarrow x=-7\) thỏa mãn bpt \(x+3< 2\) \(\left(-7< -1\right)\)
a) Đkxđ: \(x-5\ne0\Leftrightarrow x\ne5\).
b) Đkxđ: \(x\in R\).
c) Đkxđ: \(x^2-x-2\ge0\)\(\Leftrightarrow\left(x+1\right)\left(x-2\right)\ge0\)
Th1: \(\left\{{}\begin{matrix}x-1\ge0\\x-2\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x\ge2\end{matrix}\right.\)\(\Leftrightarrow x\ge2\).
Th2: \(\left\{{}\begin{matrix}x-1< 0\\x-2< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x< 1\\x< 2\end{matrix}\right.\)\(\Leftrightarrow x< 1\).
Đkxđ: \(\left[{}\begin{matrix}x\ge2\\x< 1\end{matrix}\right.\).
d) Đkxđ: \(x\in R\).
bài 2
f(x) =|...|
ghép g(x) =x^2 -2x-3
và -(x^2 -2x-3)
m<0 vô nghiệm
m=0 2 nghiệm
m=4 3 nghiệm
0<n<4 4 nghiệm
Bài 2: Restore : a;b;c không âm thỏa \(a^2+b^2+c^2=1\)
Tìm Min & Max của \(M=\left(a+b+c\right)^3+a\left(2bc-1\right)+b\left(2ac-1\right)+c\left(2ab-1\right)\)
Bài 4: Tương đương giống hôm nọ thôi : V
Bài 5 : Thiếu ĐK thì vứt luôn : V
Bài 7: Tương đương
( Hoặc có thể AM-GM khử căn , sau đó đổi \(\left(a;b;c\right)\rightarrow\left(\dfrac{x}{y};\dfrac{y}{z};\dfrac{z}{x}\right)\) rồi áp dụng bổ đề vasile)
Bài 8 : Đây là 1 dạng của BĐT hoán vị
@Ace Legona @Akai Haruma @Hung nguyen @Hà Nam Phan Đình @Neet
Nhân hai vế của bất phương trình với x ta được:\(1< x\). Bất phương trình này không tương đương với bất phương trình \(\dfrac{1}{x}< 1\) vì chưa thể khẳng định \(x>0\) mà ta phải xét hai trường hợp:
Th1: x > 0: \(Bpt\Leftrightarrow1< x\).
Th2: x < 0 \(Bpt\Leftrightarrow1>x\)
Cách 1 (đồ thị): Đầu tiên ta xác định miền nghiệm của hệ bất phương trình sau: \(\left\{{}\begin{matrix}x>0\\y>0\\\dfrac{x}{3}+\dfrac{y}{4}\le1\end{matrix}\right.\) như sau:
Sau đó ta tìm tất cả các điểm nguyên nằm ở miền trong tam giác OAB. Ta nhận thấy các điểm này là \(\left(1,1\right);\left(1,2\right);\left(2,1\right)\). Vậy các nghiệm (x; y) của bpt là \(\left(1;1\right),\left(1;2\right),\left(2;1\right)\)
Cách 2: (đại số)
Ta có \(\dfrac{x}{3}+\dfrac{y}{4}\le1\) nên \(\dfrac{x}{3}< 1\) \(\Leftrightarrow x< 3\) \(\Rightarrow x\in\left\{1,2\right\}\)
\(\dfrac{y}{4}< 1\Rightarrow y< 4\Rightarrow y\in\left\{1,2,3\right\}\)
Thử lại, ta thấy chỉ có các cặp \(\left(x;y\right)=\left(1;1\right),\left(1;2\right),\left(2;1\right)\) là thỏa mãn. Vậy...