Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=0\Leftrightarrow4x^3-4x=0\Leftrightarrow4x\left(x^2-1\right)=0\\ \Leftrightarrow x=\pm1.và.x=0\)
\(HSNB:\left(-\infty;-1\right)\cup\left(0;1\right)\\ HSĐB:\left(-1;0\right)\cup\left(1;+\infty\right)\)

Đáp án: A.
Hàm số dạng này có một điểm cực đại tại x = 0. Vậy hàm số đồng biến trên khoảng (- ∞ ; 0).

Đáp án: A.
Hàm số dạng này có một điểm cực đại tại x = 0. Vậy hàm số đồng biến trên khoảng (- ∞ ; 0).

Đáp án: A.
Hàm số nghịch biến trên từng khoảng ( - ∞ ; -m), (-m; + ∞ ) khi và chỉ khi
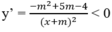
⇔ - m 2 + 5m - 4 < 0
⇔ 

a) y = x – sinx, x ∈ [0; 2π].
y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2π]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.
Vậy hàm số đồng biến trên đoạn [0; 2π].
c) Xét hàm số y = sin(1/x) với x > 0.
![]()
Giải bất phương trình sau trên khoảng (0; + ∞ ):
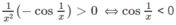
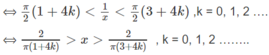
Do đó, hàm số đồng biến trên các khoảng
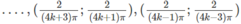
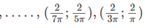
Và nghịch biến trên các khoảng
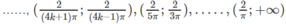
với k = 0, 1, 2 …

+ Sử dụng tính chất: Hàm số y= logax đồng biến trên TXĐ khi a> 1nên y= f(x) = lnx
là hàm số đồng biến.
+ Sử dụng tính chất: Hàm số y= ax nghịch biến trên R khi 0< a< 1nên

Chọn C

Đáp án: A.
Hàm số nghịch biến trên từng khoảng (- ∞ ; -m), (-m; + ∞ ) khi và chỉ khi
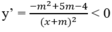
⇔ - m 2 + 5m - 4 < 0
⇔ ![]()
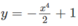 đồng biến trên khoảng:
đồng biến trên khoảng: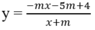
y' = 0 <=> 2 x 4 - 1 > 0 <=> x > 1/16 => Khoảng đồng biến của hàm số là 1 16 ; + ∞
Chọn C