Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$M=\frac{2x^2-3x+3}{x-2}=\frac{(2x^2-4x)+(x-2)+5}{x-2}$
$=\frac{2x(x-2)+(x-2)+5}{x-2}=2x+1+\frac{5}{x-2}$
Với $x$ nguyên, để $M$ nguyên thì $\frac{5}{x-2}$ nguyên
$\Rightarrow x-2$ là ước của $5$ (do $x$ nguyên)
$\Rightarrow x-2\in\left\{5;-5;1;-1\right\}$
$\Rightarrow x\in\left\{7; -3; 3; 1\right\}$

c) Ta có x^2 -44=x^2 -49 +5
Với x thuộc Z để x^2 -44 trên x+7 thuộc Z
Tương đương x+7 là ước của 5
Ư(5)={-5;-1;1;5}
Ta có: x+7=1 suy ra x=-6
x+7=-1 suy rax=-8
x+7=5 suy ra x=-2
x+7=-5 suy ra x=-12
a) để phân thức có giá trị nguyên thì: 5 phải chia hết cho \(2x+1\)
\(\Rightarrow2x+1\)thuộc ước của 5 gồm: -5;-1;1;5
*Với \(2x+1=-5\)ta có: \(x=-3\)
*Với \(2x+1=-1\) ta có : \(x=-1\)
*Với \(2x+1=1\) ta có :\(x=0\)
*Với \(2x+1=5\) ta có :\(x=2\)
Vậy để phân thức có giá trị nguyên thì :\(x=-3\);;\(x=-1\);;\(x=0\);;\(x=2\)..
Nhứ tích mình nha.

với m> -4 thì đa thức co nghiệm là số hữu tỷ, không lẽ bn học trg chuyên mà không hiểu?
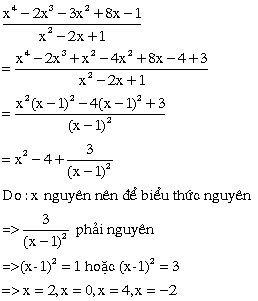
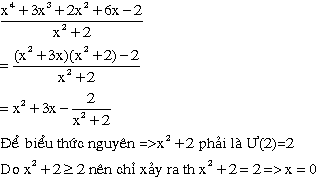 ok bn có thể xem xét mk mk ko chép mạng đâu
ok bn có thể xem xét mk mk ko chép mạng đâu