
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

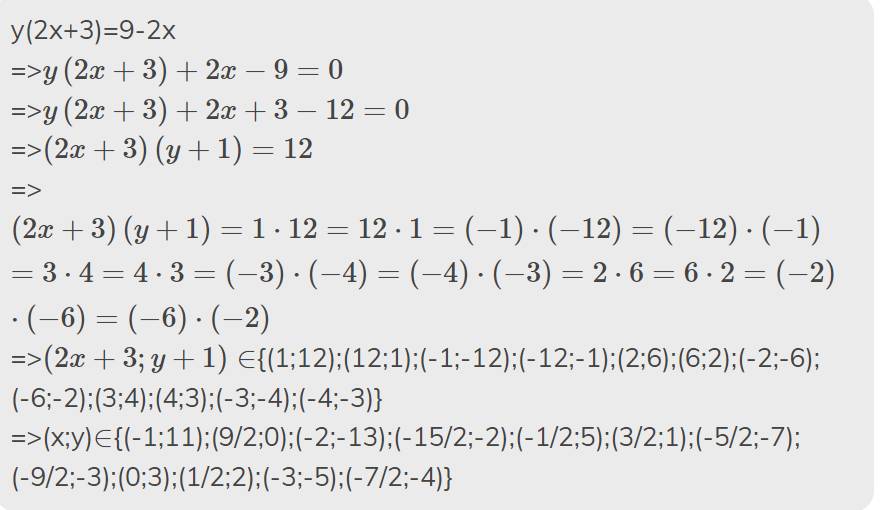

a)
x=3 y=0
b)x=1 y=1
c)x=0 y=7 mình không biết có đúng ko nữa bạn suy nghĩ xem nhé #kết bạn với mk nha# cho hỏi người lạ minhf trả lời thế có k ko <3

\(xy-2x+y=1\)
\(\Leftrightarrow x\left(y-2\right)+\left(y-2\right)=-1\)
\(\Leftrightarrow\left(x+1\right)\left(y-2\right)=-1\)
Ta có bảng sau:
| \(x+1\) | 1 | -1 |
| \(y-2\) | -1 | 1 |
| \(x\) | 0 | -2 |
| \(y\) | 1 | 3 |
Vậy ta tìm được các cặp số \(\left(0;1\right);\left(-2;3\right)\) thỏa yêu cầu bài toán.

Thêm mỗi vế 13 đơn vị, ta có:
2x-13+13=5-x+13
2x=18-x
3x=18
x=18:3
x=6
Học tốt nha em.
\(2x-13=5-x\)
\(\Rightarrow2x+x=5+13\)
\(\Rightarrow3x=18\)
\(\Rightarrow x=6\)

Tham khảo: https://olm.vn/hoi-dap/detail/103429897807.html
hok tốt!!
Ta có : x2 – 2x + 1 = 6y2 - 2x + 2
\(\Rightarrow\) x2 – 1 = 6y2 \(\Rightarrow\) 6y2 = ( x - 1 ) . ( x + 1 ) chia hết cho 2 , do 6y2 chia hết cho 2 .
Mặt khác x - 1 + x + 1 = 2x chia hết cho 2 \(\Rightarrow\) ( x - 1 ) và ( x + 1 ) cùng chẵn hoặc cùng lẻ .
Vậy ( x - 1 ) và ( x + 1 ) cùng chẵn \(\Rightarrow\) ( x - 1 ) và ( x + 1 ) là hai số chẵn liên tiếp .
( x - 1 ) . ( x + 1 ) chia hết cho 8 \(\Rightarrow\) 6y2 chia hết cho 8 \(\Rightarrow\) 3y2 chia hết cho 4 \(\Rightarrow\) y2 chia hết cho 4 \(\Rightarrow\) y chia hết cho 2
y = 2 ( y là số nguyên tố )
Tìm được x = 5 .

xy + 2x + 3y +5 = 0
x(y+2) + 3y +6 - 1 = 0
x(y+2) + 3(y+2) - 1 = 0
(y+ 2 ) (x+3) = 1
\(\Rightarrow\)y+2 và x+3 \(\in\)Ư(1) = { -1 , 1 }
ta có bảng
| y+2 | -1 | 1 |
| x+3 | -1 | 1 |
| y | -3 | -1 |
| x | -4 | -2 |
vậy (x,y) \(\in\){ (-4,-3) ; ( -2, -1 ) }

2x + 1 chia hết cho x - 1
=> 2x - 2 + 3 chia hết cho x - 1
=> 2(x-1) + 3 chia hết cho x - 1
=> 3 chia hết cho x - 1
tự xét ước
2x + 1 chia hết cho x - 2
=> 2x - 4 + 5 chia hết cho x - 2
=> 2(x-2) + 5 chia hết cho x - 2
=> 5 chia hết cho x - 2
=> ...
ban co ten giong minh va co tuoi giong minh ban hoc truong nao vay

Áp dụng bất đẳng thức \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(A\ge\left|y-1-3-y\right|=\left|-2\right|=2\)
Dấu " = " khi \(\hept{\begin{cases}y-1\ge0\\3-y\ge0\end{cases}}\Rightarrow\hept{\begin{cases}y\ge1\\y\le3\end{cases}}\Rightarrow1\le y\le3\)
Vậy \(MIN_A=2\) khi \(1\le y\le3\)