
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : 42 = 16 và (-4)2 = 16
Nên 4 và – 4 là các căn bậc hai của 16

Các số có căn bậc hai:
a = 0 c = 1 d = 16 + 9
e = 32 + 42 h = (2-11)2 i = (-5)2
l = √16 m = 34 n = 52 - 32
Căn bậc hai không âm của các số đó là:
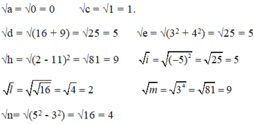


- Ta có: \(A=\frac{\sqrt{x+1}}{\sqrt{x-1}}\)
- Thay \(x=\frac{16}{9}\)vào đa thức \(A,\)ta có:
\(A=\frac{\sqrt{\frac{16}{9}+1}}{\sqrt{\frac{16}{9}-1}}\)
\(\Leftrightarrow A=\frac{\sqrt{\frac{25}{9}}}{\sqrt{\frac{7}{9}}}\)
\(\Leftrightarrow A=\frac{5\sqrt{7}}{7}\)
Vậy \(A=\frac{5\sqrt{7}}{7}\)
Thay x = 16/9 vào biểu thức, ta có:
\(\frac{\sqrt{\frac{16}{9}+1}}{\sqrt{\frac{16}{9}-1}}=\frac{\sqrt{\frac{25}{9}}}{\sqrt{\frac{7}{9}}}=\frac{\frac{5}{3}}{\frac{\sqrt{7}}{3}}=\frac{5\sqrt{7}}{5}\)

a: \(\dfrac{\sqrt{81}}{\sqrt{16}}=\dfrac{9}{4}=\dfrac{36}{16}< \dfrac{81}{16}\)
b: \(\sqrt{16+25}=\sqrt{41}< 9=\sqrt{16}+\sqrt{25}\)

a) Vì \({3^2} = 9\) và 3 > 0 nên \(\sqrt 9 = 3\)
b) Vì \({4^2} = 16\) và 4 > 0 nên \(\sqrt {16} = 4\)
c) Vì \({9^2} = 81\) và 9 > 0 nên \(\sqrt {81} = 9\)
d) Vì \({11^2} = 121\) và 11 > 0 nên \(\sqrt {121} = 11\)

\(\sqrt{16}\)= -4 và 4
Ai giúp mk mk sẽ giúp lại
Hk tốt
\(\sqrt{16}\)=4