Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Gọi 4 số phải tìm là a1, a2, a3, a4. Theo đầu bài Ta có hệ:
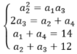
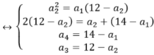
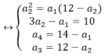
Giải các hệ phương trình Ta có kết quả a1=2, a2=4, a3=8 và a4=12
Chọn D

Chọn B.
Gọi bốn số đó là a ;b ;c ;d ta có hệ:
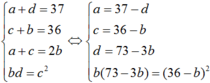
Giải ra ta được : b = 16 ; c = 20 ; d = 25 ; a = 12.

+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x
Theo giả thiết ta có hệ phương trình
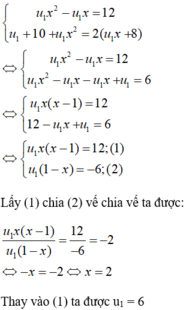
+ Tổng của năm số hạng đầu của CSN là:


Chọn B
Giả sử ba số hạng a, b, c lập thành cấp số cộng thỏa yêu cầu, khi đó b, a, c theo thứ tự đó lập thành cấp số nhân công bội q. Ta có
a + c = 2 b a = b q ; c = b q 2 ⇒ b q + b q 2 = 2 b ⇔ b = 0 q 2 + q − 2 = 0 .
Nếu b = 0 ⇒ a = b = c = 0 nên a, b, c là cấp số cộng công sai d= 0 (vô lí).
Nếu q 2 + q − 2 = 0 ⇔ q = 1 hoặc q= -2. Nếu q = 1 ⇒ a = b = c (vô lí), do đó q = -2.

Giả sử cấp số nhân có số hạng đầu \(u_1\) và công bội \(q\)
\(\Rightarrow\) Số thứ 2 và thứ 3 lần lượt là \(u_1q\) và \(u_1q^2\)
Từ dữ kiện thứ 1 ta có: \(2\left(u_1q+2\right)=u_1+u_1q^2\)
\(\Rightarrow u_1\left(q^2-2q+1\right)=4\) (1)
Từ dữ kiện thứ 2 ta có: \(u_1\left(u_1q^2+9\right)=\left(u_1q+2\right)^2\)
\(\Rightarrow\left(u_1q\right)^2+9u_1=\left(u_1q\right)^2+4u_1q+4\)
\(\Leftrightarrow u_1\left(9-4q\right)=4\) (2)
Chia vế cho vế (1) và (2):
\(\Rightarrow q^2-2q+1=9-4q\)
\(\Leftrightarrow q^2+2q-8=0\Rightarrow\left[{}\begin{matrix}q=2\Rightarrow u_1=4\\q=-4\Rightarrow u_1=\dfrac{4}{25}\end{matrix}\right.\)

Chọn A
Gọi u1,u2,u3,u4 là 4 số hạng đầu tiên của cấp số nhân, với công bội q. gọi (vn) là cấp số cộng tương ứng với công sai là d. Theo giả thuyết Ta có:
u 1 + u 2 + u 3 = 16 4 9 u 1 = v 1 u 2 = v 4 = v 1 + 3 d u 3 = v 8 = v 1 + 7 d ⇔ u 1 + u 1 q + u 2 q 2 = 16 4 9 1 u 1 q = u 1 + 3 d 2 u 1 q 2 = u 1 + 7 d 3
Khử d từ (2) và (3) ta thu được:
7 u 1 q = 7 u 1 + 21 d 3 u 1 q 2 = 3 u 1 + 21 d
Lấy vế trừ vế ta thu được
7 u 1 q − 3 u 1 q 2 = 4 u 1 ⇔ u 1 . 3 q 2 − 7 q + 4 = 0 ⇔ u 1 = 0 3 q 2 − 7 q + 4 = 0
Do u 1 ≠ 0 ⇒ q = 1 q = 4 3
Theo định nghĩa cấp số nhận thì q ≠ 1 . Do đó q = 4 3
Thay q = 4 3 vào (1) ta được u 1 = 4

Tổng số lương của chuyên gia đó sau 10 năm là:
\(S=\dfrac{10\cdot\left[2\cdot240+10\cdot1.05\right]}{2}=2452.5\left(đồng\right)\)
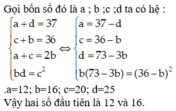
Gọi 4 số cần tìm là \(a_1,a_2,a_3,a_4\). Theo đầu bài ta có hệ :
\(\begin{cases}a_2^2=a_1a_3\\2a_3=a_2+a_4\\a_1+a_4=14\\a_2+a_3=12\end{cases}\) \(\Leftrightarrow\begin{cases}2a_1q^2=a_1q+a_2+d\left(1\right)\\a_1+a_2+d=14\left(2\right)\\a_1q+a_1q^2=12\left(3\right)\\a_2+a_2+d=12\left(4\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}a_2^2=a_1\left(a_2+d\right)\left(5\right)\\a_2+2d=14-a_1\\a_1=\frac{12}{q+q^2}\\d=12-2a_2\end{cases}\)
Giải hệ thống các phương trình ta có kết quả \(\left(2,4,8,12\right)\left(\frac{25}{2},\frac{15}{2}\frac{9}{2}\frac{3}{2}\right)\)