PQ
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 6 2021
Vì :
100 = 22 x 52
36 = 22 x 32
=> BCNN ( 100 , 36 ) = 22 x 32 x 52 = 900
TT
6 tháng 6 2021
Ta có:
100 = 22 x 52
36 = 22 x 32
\(\Rightarrow\)BCNN(100,36) = 22 x 52 x 32 = 900
TA
5 tháng 8 2021
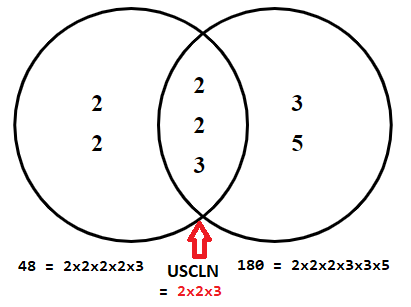
2.2.3=12.USCLN (12) :2;3;4;6;12;1
BSCLN:(1;2;3...............)
Chúc bạn học tốt nha
LM
28 tháng 10 2021
TL:
2.2.3=12.USCLN (12) :2;3;4;6;12;1
BSCLN:(1;2;3...............)
^H T^
HH
29 tháng 4 2017
Gọi (a;b) = d (\(d\in N\))
Ta có: \(a+2b=49\)
Vì \(a⋮d\) và \(b⋮d\) nên suy ra \(a+2b⋮d\)
\(\Rightarrow49⋮d\left(1\right)\)
Lại có: \(\left[a;b\right]+\left(a;b\right)=\left[a;b\right]+d=56\)
Vì \(a⋮d;b⋮d\) \(\Rightarrow\left[a;b\right]⋮d\)
\(\Rightarrow\left[a;b\right]+d⋮d\)
\(\Rightarrow56⋮d\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta suy ra \(d\inƯC\left(49;56\right)\)
\(\Rightarrow d\in\left\{1;7\right\}\) (Vì d là số tự nhiên)
+) Với d = 1 thì \(\left[a;b\right]+1=56\)
\(\Rightarrow\left[a;b\right]=55\)
\(\Rightarrow a.b=55\)
Ta có bảng sau:
| a | 1 | 55 | 5 | 11 |
| b | 55 | 1 | 11 | 5 |
Thử các giá trị trên vào a + 2b = 49 đều không thỏa mãn.(loại d = 1)
+) Với d = 7 \(\Rightarrow ab=7.\left[a;b\right]\)
\(\Rightarrow a=7m;b=7n\left(m;n\in N\right)\) \(\left(m;n\right)=1\)
\(\Rightarrow mn=7\)
+) Nếu m = 1; n = 7 thì a = 7; b = 49 (loại)
+) Nếu m = 7; n = 49 thì a = 49; b = 7 (loại)
\(\Rightarrow\) Loại trường hợp d = 7
Vậy không có số tự nhiên a và b nào thỏa mãn đề bài.
NN
0
10 tháng 5 2016
a)A=(x-1)2+12
Ta có (x-1)2\(\ge\)0
=>A=(x-1)2+12\(\ge\)12
Dấu "=" xảy ra khi x-1=0 =>x=1
Vậy GTNN của A là 12 tại x=1
b) B=|x+3|+2016
Ta có: |x+3|\(\ge\)0
=>B=|x+3|+2016\(\ge\)2016
Dấu "=' xảy ra khi x+3=0 =>x=-3
Vậy GTNN của B là 2016 tại x=-3
c)C=\(\frac{x+5}{x-4}=\frac{x-4}{x-4}+\frac{9}{x-4}=1+\frac{9}{x-4}\)
Để C có GTNN thì: \(\frac{9}{x-4}\) có GTNN
=>x-4 có là số nguyên âm lớn nhất
=>x-4=-1 =>x=3
Vậy x=3 thì C có giá trị nhỏ nhất là: \(1+\frac{9}{-1}=-8\)
NN
29 tháng 6 2016
Vì \(\frac{15}{x}+4\) là số nguyên
\(\Rightarrow15⋮x\)(hoặc \(x\inƯ\left(15\right)\)
Vậy Ư(15)là:[1,-1,3,-3,5,-5,15,-15]
Do đó \(x\in\)[1,-1,3,-3,5,-5,15,-15]
29 tháng 6 2016
để phân số trên là số nguyên thì (x+4) thuộc Ư(15)={1,3,5,-1,-3,-5,15,-15}
xét từng TH:
x+4=1=>x=-3
x+4=3=>x=-1
x+4=5=>x=1
x+4=15=>x=11
x+4=-1=>x=-5
x+4=-3=>x=-7
x+4=-5=>x=-9
x+4=-15=>x=-19
vậy x thuộc { -19,-9,-7,-5,-1,1,11,-3}
NV
2
22 tháng 2 2021
Vì 7c là bội của c - 2 nên:
\(\Rightarrow\)\(7c⋮c-2\)
Ta có: \(7c=7c-14+14=7.\left(c-2\right)+14\)
Để \(7c⋮c-2\)\(\Leftrightarrow\)\(7.\left(c-2\right)+14⋮c-2\)mà \(7.\left(c-2\right)⋮c-2\)
\(\Rightarrow\)\(14⋮c-2\)\(\Rightarrow\)\(c-2\inƯ\left(14\right)\in\left\{\pm1;\pm2;\pm7;\pm14\right\}\)
\(\Rightarrow\)\(c\in\left\{1;3;0;4;-5;9;-12;16\right\}\)( các giá trị trên đều thoả mãn )
Vậy \(c\in\left\{1;3;0;4;-5;9;-12;16\right\}\)
26 tháng 1 2021
thằng thiên sơn trả lời hộ taoooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooo
26 tháng 1 2021
Ta có: \(A=\frac{6x+49}{x+5}=\frac{\left(6x+30\right)+19}{x+5}=\frac{6\left(x+5\right)+19}{x+5}=6+\frac{19}{x+5}\)
Để 6x+49 là bội số của x+5 thì A nguyên
=> \(\frac{19}{x+5}\inℤ\Rightarrow x+5\inƯ\left(19\right)=\left\{\pm1;\pm19\right\}\)
\(\Rightarrow x\in\left\{-24;-6;-4;14\right\}\)
Vậy \(x\in\left\{-24;-6;-4;14\right\}\)
TC
21 tháng 3 2021
Ta có: 7b+2⋮b−2
⇔7b−14+16⋮b−2
mà 7b−14⋮b−2
nên 16⋮b−2
⇔b−2∈Ư(16)
⇔b−2∈{1;−1;2;−2;4;−4;8;−8;16;−16}
hay b∈{3;1;4;0;6;−2;10;−6;18;−14}
Vậy: b∈{3;1;4;0;6;−2;10;−6;18;−14}
BCNN(36,70)=2