tìm biểu thức và chứng minh bằng phương pháp quy nap

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Phan Thành Quân

23 tháng 9 2022 - olm

tìm biểu thức và chứng minh bằng phương pháp quy nap

#Toán lớp 11

Phan Thành Quân

24 tháng 9 2022

Đúng(1)

Phan Thành Quân

23 tháng 9 2022

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

20 tháng 8 2018

Cho tổng: S n = 1 1 . 5 + 1 5 . 9 + . . . + 1 4 n - 3 4 n + 1 a) Tính S 1 , S 2 , S 3 , S 4 ; b) Dự đoán công thức tính S n và chứng minh bằng phương pháp quy...

Đọc tiếp

#Toán lớp 11

Cao Minh Tâm

20 tháng 8 2018

a) Tính

Giải sách bài tập Toán 11 | Giải sbt Toán 11

b) Viết lại

Giải sách bài tập Toán 11 | Giải sbt Toán 11

Ta có thể dự đoán Giải sách bài tập Toán 11 | Giải sbt Toán 11

Đúng(0)

Thanhtung Phan

31 tháng 10 2023 - olm

Chứng minh Công thức sau bằng phương pháp Quy nạp.

$S_n$= $\dfrac{u_1\left(1-q^n\right)}{1-q}$

#Toán lớp 11

Akai Haruma

Giáo viên

31 tháng 10 2023

Lời giải:

Tổng của $n$ số hạng trong dãy là cấp số nhân $(u_n)$ với công bội $q$ là:

$S_n=u_1+u_2+....+u_n=u_1+u_1q+u_1q^2+...+u_1q^{n-1}$

$=u_1(1+q+q^2+....+q^{n-1})$

$qS_n=u_1(q+q^2+q^3+...+q^n)$

$\Rightarrow qS_n-S_n=u_1(q+q^2+q^3+...+q^n)-u_1(1+q+q^2+....+q^{n-1})$

$\Rightarrow S_n(q-1)=u_1(q^n-1)$

$\Rightarrow S_n=\frac{u_1(q^n-1)}{q-1}=\frac{u_1(1-q^n)}{1-q}$

Ta có đpcm.

Đúng(2)

Hiệu Bùi Đức

29 tháng 11 2021

Chứng minh các đẳng thức, mệnh đề sau bằng phương pháp quy nạp toán học: (n⁶-3n⁵+6n⁴-7n³+5n²-2n) chia hết 24

#Toán lớp 11

Nguyễn Hoàng Minh

29 tháng 11 2021

Với $n=0\Rightarrow0-0+0-0+0-0=0⋮24\left(đúng\right)$

Với $n=1\Rightarrow1-3+6-7+5-2=0⋮24\left(đúng\right)$

G/s $n=k\Rightarrow\left(k^6-3k^5+6k^4-7k^3+5k^2-2k\right)⋮24$

$\Rightarrow k\left(k^5-3k^4+6k^3-7k^2+5k-2\right)⋮24\\ \Rightarrow k\left(k+1\right)\left(k^2+k+1\right)\left(k^2-k+2\right)⋮24$

Với $n=k+1$, ta cần cm $\left[\left(k+1\right)^6-3\left(k+1\right)^5+6\left(k+1\right)^4-7\left(k+1\right)^3+5\left(k+1\right)^2-2\left(k+1\right)\right]⋮24$

Ta có $\left(k+1\right)^6-3\left(k+1\right)^5+6\left(k+1\right)^4-7\left(k+1\right)^3+5\left(k+1\right)^2-2\left(k+1\right)$

$=\left(k+1\right)\left[\left(k+1\right)^5-3\left(k+1\right)^4+6\left(k+1\right)^3-7\left(k+1\right)+5\left(k+1\right)-2\right]\\ =\left(k+1\right)\left(k+1-1\right)\left[\left(k+1\right)^2-\left(k+1\right)+1\right]\left[\left(k+1\right)^2-\left(k+1\right)+2\right]\\ =k\left(k+1\right)\left(k^2+k+1\right)\left(k^2+k+2\right)$

Mà theo GT quy nạp ta có $k\left(k+1\right)\left(k^2+k+1\right)\left(k^2+k+2\right)⋮24$

Vậy ta được đpcm

Đúng(1)

Hiệu Bùi Đức

29 tháng 11 2021

Chứng minh các đẳng thức, mệnh đề sau bằng phương pháp quy nạp toán học:

(n⁶-3n⁵+6n⁴-7n³+5n²-2n):24(13ⁿ-1):6

#Toán lớp 11

Pham Trong Bach

21 tháng 9 2019

Dãy số u n cho bởi u 1 = 3 , u n + 1 = 1 + u n 2 , n > 1 a. Viết năm số hạng đầu của dãy số.b. Dự đoán công thức số hạng tổng quát un và chứng minh công thức đó bằng phương pháp quy...

Đọc tiếp

#Toán lớp 11

Cao Minh Tâm

21 tháng 9 2019

a. Năm số hạng đầu của dãy số

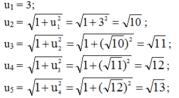
Giải bài tập Đại số 11 | Để học tốt Toán 11

b. Dự đoán công thức số hạng tổng quát của dãy số:

un =√(n+8) (1)

Rõ ràng (1) đúng với n = 1

Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)

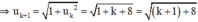
Giải bài tập Đại số 11 | Để học tốt Toán 11

⇒ (1) đúng với n = k + 1

⇒ (1) đúng với mọi n ∈ N*.

Đúng(0)

Pham Trong Bach

12 tháng 1 2019

Chứng minh bằng phương pháp quy nạp n 3 + 11 n chia hết cho 6.

#Toán lớp 11

Cao Minh Tâm

12 tháng 1 2019

* Với n =1 ta có 1 3 + 11.1 = 12 chia hết cho 6 đúng.

* Giả sử với n = k thì k 3 + 11 k chia hết cho 6.

* Ta phải chứng minh với n =k+1 thì ( k + 1 ) 3 + 11(k +1) chia hết cho 6.

Thật vậy ta có :

k + 1 3 + 11 k + 1 = k 3 + 3 k 2 + 3 k + 1 + 11 k + 11 = ( k 3 + 11 k ) + 3 k ( k + 1 ) + 12 *

Ta có; k 3 +11k chia hết cho 6 theo bước 2.

k(k+1) là tích 2 số tự nhiên liên tiếp nên chia hết cho 2 ⇒ 3 k ( k + 1 ) ⋮ 6

Và 12 hiển nhiên chia hết cho 6.

Từ đó suy ra (*) chia hết cho 6 (đpcm).

Đúng(0)

Pham Trong Bach

28 tháng 3 2018

Cho hai số 3 n và 8n với n ∈ N * .

a) So sánh 3 n và 8n khi n = 1 , 2 , 3 , 4 , 5 .

b) Dự đoán kết quả tổng quát và chứng minh bằng phương pháp quy nạp

#Toán lớp 11

Cao Minh Tâm

28 tháng 3 2018

a)n = 1 ⇒ 31 = 3 < 8 = 8.1

n = 2 ⇒ 32 = 9 < 16 = 8.2

n = 3 ⇒ 33 = 27 > 24 = 8.3

n = 4 ⇒ 34 = 81 > 32 = 8.4

n = 5 ⇒ 35 = 243 > 40 = 8.5

b) Dự đoán kết quả tổng quát: 3n > 8n với mọi n ≥ 3

- n = 3, bất đẳng thức đúng

- Giả sử bất đẳng thức đúng với n = k ≥ 3, nghĩa là:

3k > 8k

Ta phải chứng minh rằng bất đẳng thức cũng đúng với n = k + 1, tức là:

3(k + 1) > 8(k + 1)

Thật vậy, từ giả thiết quy nạp ta có:

3(k + 1) = 3k.3 > 8k.3 = 24k = 8k + 16k

k ≥ 3 ⇒ 16k ≥ 16.3 = 48 > 8

Suy ra: 3(k + 1) > 8k + 8 = 8(k + 1)

Vậy bất đẳng thức đúng với mọi n ≥ 3

Đúng(0)

Big City Boy

10 tháng 9 2023

Chứng minh bằng phương pháp quy nạp toán học: $\forall n\in N$*, ta luôn có: $sin^{2n}\alpha+cos^{2n}\alpha\le1$

#Toán lớp 11

Đức Anh 2k9

29 tháng 8 2021 - olm

Chứng minh rằng:

$n^n\ge\left(n+1\right)^{n-1}\forall n\inℕ^∗$

Chứng minh bằng phương pháp quy nạp nhé

#Toán lớp 11

Mai Anh Nguyen

29 tháng 8 2021

Với n = 1 thì $x^1\ge2.x^0=0$

Giả sử đẳng thức đúng với n = k nghĩa là : $x^k\ge\left(k+1\right).x^{k-1}$.

Ta phải chứng minh :

$x^n\ge\left(n+1\right).x^{n-1}$đúng với n = k + 1. Ta phải chứng minh $x^{k+1}\ge\left[\left(k+1\right)+1\right].x^{\left(k-1\right)+1}=\left(k+2\right).x^k$

$=\left(x^k.k+2x^k+1\right)-1=\left(x^k+1\right)^2-1\le x^{k+1}$

Vậy đẳng thức luôn đúng với mọi $n\inℕ^∗$

Đúng(0)

Phan Thanh Tùng

2 tháng 11 2023 - olm

Chứng minh công thúc Tổng của một cấp số nhân bằng phương pháp Quy nạp.

$S_n=\dfrac{U_1\left(1-q^n\right)}{1-q}$

#Toán lớp 11

Akai Haruma

Giáo viên

4 tháng 11 2023

Lời giải:
Xét csn $(u_n)$ với công bội $q$

Ta có:

$S_n=u_1+u_2+...+u_n=u_1+u_1q+u_1q^2+....+u_1q^{n-1}$

$=u_1(1+q+q^2+....+q^{n-1})$

$qS_n=u_1(q+q^2+q^3+....+q^n)$

$\Rightarrow qS_n-S_n=u_1(q^n-1)$

$\Rightarrow S_n(q-1)=u_1(q^n-1)$

$\Rightarrow S_n=\frac{u_1(q^n-1)}{q-1}=\frac{u_1(1-q^n)}{1-q}$

Ta có đpcm.

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP