
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

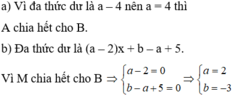

a) \(x^3+x^2-x+a=\left(x^2-x+1\right)\left(x+2\right)+\left(a-2\right)\).
Đa thức trên chia hết cho \(x+2\) khi và chỉ khi a = 2.
b) \(x^3+ax^2+2x+b=\left(x^2+x+1\right)\left(x+1\right)+\left(a-2\right)x^2+\left(b-1\right)\) chia hết cho \(x^2+x+1\) khi và chỉ khi:
\(\frac{a-2}{1}=\frac{0}{1}=\frac{b-1}{1}\Leftrightarrow a=2;b=1\).
c) Tương tự.

a: \(\Leftrightarrow x^4-x^3-2x^2-8x^3+8x^2+16x+15x^2-15x-30+a+30⋮x^2-x-2\)
=>a+30=0
=>a=-30
b: \(\Leftrightarrow2x^4-4x^2+4x^2-8+ax+b+8⋮x^2-2\)
=>a=0 và b=-8

Bài 1 :
b, Ta có : \(4x^2-25-\left(2x-5\right)\left(2x+7\right)\)
\(=\left(2x-5\right)\left(2x+5\right)-\left(2x-5\right)\left(2x+7\right)\)
\(=\left(2x-5\right)\left(2x+5-2x-7\right)\)
\(=-2\left(2x-5\right)\)
c, Ta có : \(x^3+27+\left(x+3\right)\left(x-9\right)\)
\(=\left(x+3\right)\left(x^2-3x+9\right)+\left(x+3\right)\left(x-9\right)\)
\(=\left(x+3\right)\left(x^2-3x+9+x-9\right)\)
\(=x\left(x+3\right)\left(x-2\right)\)
Bài 2 :
a, Để \(x^3+3x^2+3x-2⋮x+1\)
<=> \(x^3+1+3x^2+3x-3⋮x+1\)
<=> \(\left(x+1\right)^3-3⋮x+1\)
Ta thấy : \(\left(x+1\right)^3⋮x+1\)
<=> \(-3⋮x+1\)
<=> \(x+1\inƯ_{\left(3\right)}\)
<=> \(x+1=\left\{1,-1,3,-3\right\}\)
<=> \(x=\left\{0,-2,2,-4\right\}\)
Vậy ...
b, Để \(2x^2+x-7⋮x-2\)
<=> \(2x^2-8x+8+9x-15⋮x-2\)
<=> \(2\left(x-2\right)^2+9x-15⋮x-2\)
Ta thấy : \(2\left(x-2\right)^2⋮x-2\)
<=> \(9x-15⋮x-2\)
<=> \(9x-18+3⋮x-2\)
Ta thấy : \(8\left(x-2\right)⋮x-2\)
<=> \(3⋮x-2\)
<=> \(x-2\inƯ_{\left(3\right)}\)
<=> \(x-2=\left\{1,-1,3,-3\right\}\)
<=> \(x=\left\{3,1,5,-1\right\}\)
Vậy ...

a) Dư của f(x ) chia cho x+2 là f(-2)
Áp dụng định lý Bơ-zu ta có :
\(f\left(-2\right)=\left(-2\right)^3+3.\left(-2\right)^2+a\)
\(=-8+12+a\)
\(=4+a\)
\(\Leftrightarrow a=-4\)
Vậy để f(x) chia hết cho x+2 => a= -4
b) Dư của f(x ) chia cho x-1 là f(1)
Áp dụng định lí Bơ-zu ta có :
\(f\left(1\right)=1^2-3.1+a\)
\(=1-3+a\)
\(=-2+a\)
\(\Rightarrow a=2\)
Vậy ..............
c)
Đặt phép chia dọc theo đa thức 1 biến đã sắp xếp
d) Theo định lí Bơ-zu ta có :
\(f\left(x\right):x+1\)có dư là \(f\left(-1\right)\)
\(f\left(-1\right)=\left(-1\right)^3+a.\left(-1\right)+b\)
\(=-a+b-1\)
Mà theo đề bài cho dư = 7
\(\Rightarrow-a+b-1=7\)
\(\Rightarrow-a+b=8\) (1)
Tương tự :
\(f\left(x\right):x-1\)có dư là \(f\left(1\right)\)
\(f\left(1\right)=1^3+a.1+b\)
\(=a+b+1\)
Theo đề bài cho dư 7
\(\Rightarrow a+b+1=7\)
\(\Rightarrow a+b=6\)(2)
Từ (1) và (2) ( cộng vế với vế)
\(\Rightarrow\hept{\begin{cases}a+b=6\\-a+b=8\end{cases}}\)
\(\Rightarrow2b=14\)
\(\Rightarrow b=7\)
\(\Leftrightarrow a+7=6\)
\(\Rightarrow a=-1\)
Vậy \(f\left(x\right)=x^3-x+7\)