Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các số lẻ có 2 chữ số giống nhau là:
11 , 33 , 55 , 77 , 99 .
Ta thấy mỗi số hơn kém nhau 22 đơn vị (33-11=22.......)
Số lượng số hạng là:
(99-11):22+1=5(số)
Tống của tất cả các số lẻ có 2 chữ số giống nhau là :
(99+11)x5:2=275
Tổng của tất cả các số lẻ có 2 chữ số giống nhau được gấp lên 9 lần là :
275x9=2475

Ta có: a:b=\(\frac{2}{7}\)=>a=\(\frac{2}{7}\)*b
Ta có:\(\frac{a+35}{b}\)=\(\frac{11}{14}\)
=>(a+35)*14=11b
=>14a+490=11b
=>14*\(\frac{2}{7}\)*b+490=11b
=>4b+490=11b
=>490=11b-4b
=>490=7b
=>b=490:7
=>b=70
=>a=70*\(\frac{2}{7}\)
=>a=20
Vậy a=20;b=70(Đề là thêm 35 đơn vị vào a;còn lại giữ nguyên)

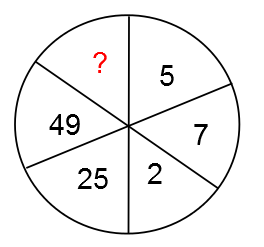
Theo đề bài ta nhận thấy số đối diện số 5 là số 25
=> Quy luật là : n2
=> 52 = 25
=> 72 = 49
<=> 22 = 4

Mình giải được phần 1 rồi nhưng không biết cách viết bài giải để gửi cho bn :))), theo mình thì phần 1 bạn chuyển căn thứ nhất với căn thứ 3 thành 1 cặp, căn thứ hai với căn thứ tư thành một cặp sau đó nhân liên hợp nhé!

Mệnh đề, tập hợp
Trong các mệnh đề sau, mệnh đề nào đúng:
- 1794 chia hết cho
- 3 π<3.15 (chọn)
- 2√ là số hữu tỉ
- Em trả lời rồi có được 3GP không học24


Ba số tự nhiên lẻ liên tiếp đều là số nguyên tố là :
3 ; 5 ; 7