Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
+ Vị trí trùng màu với vân trung tâm là vị trí trùng nhau của vân sáng 3 bức xạ :
x 1 = x 2 = x 3 ↔ 4 k 1 = 5 k 2 = 6 k 3
→ Vị trí trùng nhau gần vân trung tâm nhất ứng với k 1 = 15, k 2 = 12 và k 3 = 10
+ Sự trùng nhau của hai bức xạ λ 1 và λ 2 trong khoảng này
x 1 = x 2 ⇔ k 1 k 2 = λ 2 λ 1 = 5 4 → có 2 vị trí trùng nhau của hai hệ vân ứng với k 1 = 5và k 1 =10
+ Sự trùng nhau của hai bức xạ λ 1 và λ 3 trong khoảng này :
x 1 = x 3 ⇔ k 1 k 3 = λ 3 λ 1 = 3 2 → có 4 vị trí trùng nhau của hai hệ vân ứng với k 1 = 3, k 1 = 6, k 1 = 9 và k 1 = 12.
+ Sự trùng nhau của hai bức xạ λ 2 và λ 3 trong khoảng này :
x 2 = x 3 ⇔ k 2 k 3 = λ 3 λ 2 = 6 5 → có 1 vị trí trùng nhau của hai hệ vân ứng với k 1 = 6
Vậy số vị trí cho vân không đơn sắc là 7
Từ (1); (2); (3) ta được tỷ lệ trên
Số vân sáng đơn sắc cần tìm là
=16
Khoảng cách giữa 2 vân gần nhất có màu giống vân trung tâm là \(x_{\equiv}\)
\(\Rightarrow x_{\equiv}=k_1i_1=k_2i_2=k_3i_3\)\(\Rightarrow k_1\lambda_1=k_2\lambda_2=k_3\lambda_3\)(1)
Ta có: \(\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{5}{4}\)
Vì trong khoảng giữa hai vân sáng gần nhau nhất cùng màu với vân trung tâm chỉ có một vị trí trùng nhau của các vân sáng ứng với hai bức xạ λ1, λ2 nên: \(\begin{cases}k_1=5.2=10\\k_2=4.2=8\end{cases}\)
Thay vào (1) ta có: \(10\lambda_1=8\lambda_2=k_3\lambda_3\)
λ3 có màu đỏ nên λ1 > λ2
\(\Rightarrow k_3
Ý này của bạn bị nhầm λ3 có màu đỏ nên λ1 > λ2
Sửa lại là: Vì \(\lambda_3\) có màu đỏ nên \(\lambda_3>\lambda_2\)
Phương pháp:
Khoảng vân i = λD/a là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp.
Cách giải:
Khoảng vân:
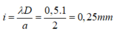
Khoảng cách giữa vân sáng bậc 3 và vân sáng bậc 5 ở hai bên vân trung tâm là: d = 3i + 5i = 8i = 2 mm
Chọn B
\(i=\dfrac{\lambda D}{a}=\dfrac{0,5\cdot10^{-6}\cdot1}{2\cdot10^{-3}}=2,5\cdot10^{-4}m=0,25mm\)
Khoảng cách từ vân sáng bậc 5 đến vân tối thứ 7 ở hai bên vân sáng trung tâm là:
\(\Delta i=5i+6,5i=11,5i=11,5\cdot0,25=2,875mm\)
Chọn A.
Chọn A
Ta có: 
= 1,25mm.
Số vân sáng trong đoạn MN là:
OM/i < k < ON/i =>3,2< k < 14,4
=> Có 11 giá trị của k thỏa mãn.
Vậy có 11 vân sáng.
Đáp án C
Ba vân trùng nhau nên ta có x1 = x2 = x3
Vậy tại vị trí trùng nhau đầu tiên của 3 bức xạ tính từ vân trung tâm thì đó là vân sáng bậc 15 của λ1, vân sáng bậc 12 của λ2 và vân sáng bậc 10 của λ3.
Xét các vị trí trùng nhau của λ1 và λ2: 
Vậy với các giá trị của k1 chia hết cho 5 thì là giá trị của k ứng với vị trí trùng nhau của λ1 và λ2 => có 2 vân trùng.
Xét các vị trí trùng nhau của λ1 và λ3: 
Vậy với các giá trị của k1 chia hết cho 3 thì là giá trị của k ứng với vị trí trùng nhau của λ1 và λ3 => có 4 vân trùng.
Xét các vị trí trùng nhau của λ3 và λ2: 
Vậy với các giá trị của k2 chia hết cho 6 thì là giá trị của k ứng với vị trí trùng nhau của λ3 và λ2 => có 1 vân trùng.
Vậy số vân sáng quan sát được trong khoảng giữa hai vân trùng nhau của 3 bức xạ là: 14 + 11 + 9 – 2 – 4 – 1 = 27 vân sáng.
