Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

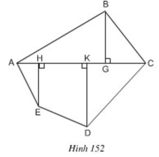
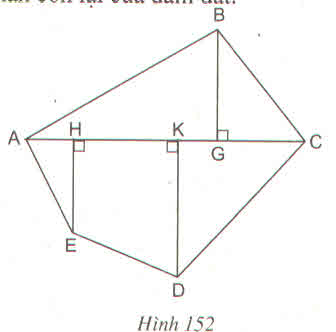
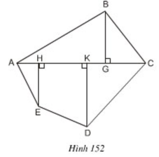
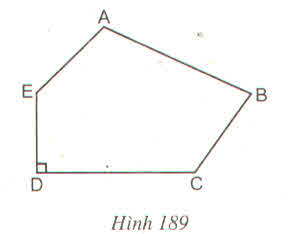
Đa giác ABCDE được chia thành tam giác ABC, hai tam giác vuông AHE, DKC và hình vuông HKDE.
Thực hiện phép đo chính xác đến mm ta được:
BG= 19mm, AC = 48mm, AH = 8mm, HK = 18mm
KC = 22mm, EH = 16mm, KD = 23mm
Nên SABC = \(\dfrac{1}{2}\).BG. AC = \(\dfrac{1}{2}\) 19.48 = 456 (mm2)
SAHE = 1212 AH. HE =\(\dfrac{1}{2}\)8.16 = 64 (mm2)
SDKC = \(\dfrac{1}{2}\) KC.KD = \(\dfrac{1}{2}\)22.23 = 253(mm2)
SHKDE = (HE+KD).HK2(HE+KD).HK2 = (16+23).182(16+23).182= 351 (mm2)
Do đó
SABCDE = SABC + SAHE + SDKC + SHKDE = 456 + 64 + 253+ 351
Vậy SABCDE = 1124(mm2)

Đa giác ABCDE được chia thành tam giác ABC, hai tam giác vuông AHE, DKC và hình vuông HKDE.
Thực hiện phép đo chính xác đến mm ta được:
BG= 19mm, AC = 48mm, AH = 8mm, HK = 18mm
KC = 22mm, EH = 16mm, KD = 23mm
Nên SABC = 1/2.BG. AC = 1/2. 19.48 = 456 (mm2)
SAHE = 1/2 AH. HE = 1/2. 8.16 = 64 (mm2)
SDKC = 1/2 KC.KD = 1/2. 22.23 = 253(mm2)
SHKDE = (HE + KD).HK / 2 = (16 + 23).18 / 2= 351 (mm2)
Do đó
SABCDE = SABC + SAHE + SDKC + SHKDE = 456 + 64 + 253+ 351
Vậy SABCDE = 1124(mm2)

Đa giác ABCDE được chia thành tam giác ABC, hai tam giác vuông AHE, DKC và hình thang vuông HKDE.
Thực hiện phép đo chính xác đến mm ta được:
BG = 19mm, AC = 48mm, AH = 8mm, HK = 18mm
KC = 22mm, EH = 16mm, KD = 23mm
Nên:

Do đó SABCDE = SABC + SAHE + SDKC + SHKDE = 456 + 64 + 253 + 351 = 1124 mm2
Vậy SABCDE = 1124 mm2



-
Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
- Chứng Tỏ Rằng J Hả Bạn ??????

A B E D H C
(Hình ảnh chỉ mang tính chất minh họa )
Giải:
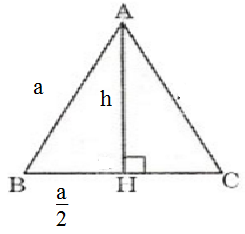
Chia thành tam giác AEB và tứ giác EDCB
kẽ AH\(\perp EB\left(H\in EB\right)\)
Ta đo được: ED=1,5 (cm) , EB=4(cm) , CD=3(cm) , AH= 1,2(cm)
SAEB=\(\dfrac{AH.EB}{2}=\dfrac{1,2.4}{2}=2,4\left(cm^2\right)\)
SEBCD=\(\dfrac{\left(EB+DC\right).ED}{2}=\dfrac{\left(4+3\right).1,5}{2}=5,25\left(cm^2\right)\)
=> SABCDE= SAEB+SEBCD=2,4 + 5,25=7,65(cm2)

\(\left(\frac{1}{2}xy-1\right).\left(x^3-2x-6\right)=\frac{1}{2}xy.\left(x^3-2x-6\right)+\left(-1\right).\left(x^3-2x-6\right)\)
= \(\frac{1}{2}xy.x^3+\frac{1}{2}xy.\left(-2x\right)+\frac{1}{2xy}.\left(-6\right)+\left(-1\right).x^3+\left(-1\right).\left(-2x\right)+\left(-1\right).\left(-6\right)\)
= \(\frac{1}{2}x^{\left(1+3\right)}y-x^{\left(1+1\right)}y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^2y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^3-x^2y-3xy+2x+6\)
Chúc bạn học tốt !!!
Bài làm
Ta có: ( xy - 1 )( x3 - 2x - 6 )
= ( xy . x3 ) + [ xy . ( -2x ) ] + [ xy . ( - 6 ) ] + [ ( -1 ) . x3 ] + [ ( -1 ) . ( -2x ) ] + [ ( -1 ) . ( -6 ) ] ( * chỗ này nếu thầnh thạo phép nnhân đa thức r thì k cần pk ghi đâu )
= x4y - 2x2y - 6xy - x3 + 2x + 6
# Học tốt #
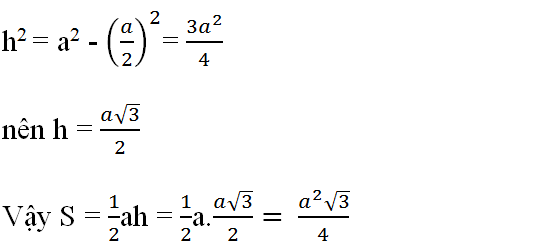
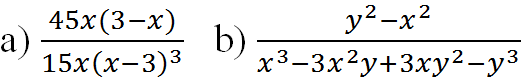
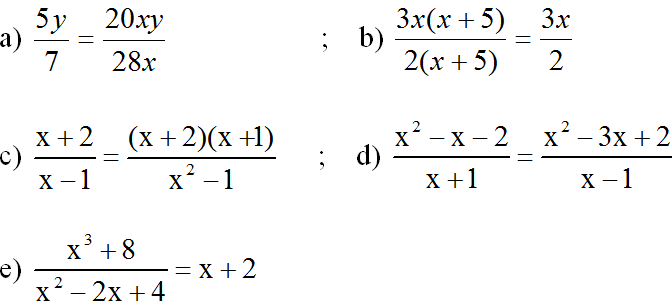

 xy – 1 với đa thức x3 – 2x – 6.
xy – 1 với đa thức x3 – 2x – 6.
Đa giác ABCDE được chia thành tam giác ABC, hai tam giác vuông AHE, DKC và hình thang vuông HKDE.
Thực hiện phép đo chính xác đến mm ta được:
BG = 19mm, AC = 48mm, AH = 8mm, HK = 18mm
KC = 22mm, EH = 16mm, KD = 23mm
Nên:
Do đó S A B C D E = S A B C + S A H E + S D K C + S H K D E = 456 + 64 + 253 + 351 = 1124 m m 2
Vậy S A B C D E = 1124 m m 2