K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VL
2
NV
10 tháng 6 2016
Ta có: 3x2 - 2(x2 + 4x) + 3x + 2 = 0
=> 3x2 - 2x2 - 8x + 3x + 2 = 0
=> x2 - 5x + 2 =0
10 tháng 6 2016
\(3x^2-2\left(x^2+4x\right)+3x+2=0\)
,<=> \(3x^2-2x^2-8x+3x+2=0\)
<=> \(x^2-5x+2=0\)
MH
18 tháng 9 2021
\(\sqrt{\left(120-11\right)^2}+\sqrt{\left(10-\sqrt{120}\right)^2}\)
\(=120-11+10+\sqrt{120}\)
\(=\sqrt{120}\left(\sqrt{120}+1\right)-1\)
18 tháng 9 2021
\(a,=\left(120-11\right)+\left|10-\sqrt{120}\right|=109+\sqrt{120}-10=99+2\sqrt{30}\\ b,=\sqrt{\left(\sqrt{x+1}+1\right)^2-\left(\sqrt{x+1}+1\right)^2}=\sqrt{0}=0\)
7 tháng 6 2022
Câu 1:
a: \(A=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=2\sqrt{x}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}=2\sqrt{x}+2\)
b: Để A=4 thì \(2\sqrt{x}=2\)
=>x=1(loại)
AT
30 tháng 7 2021
\(A=\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}+\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}+\dfrac{x+1}{\sqrt{x}}\left(x>0,x\ne1\right)\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x+1}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}+\dfrac{x-\sqrt{x}+1}{\sqrt{x}}+\dfrac{x+1}{\sqrt{x}}=\dfrac{3x+3}{\sqrt{x}}\)
\(A-\left|A\right|=0\Rightarrow A=\left|A\right|\Rightarrow\left[{}\begin{matrix}A=A\\A=-A\end{matrix}\right.\)
mà \(x>0\Rightarrow A>0\Rightarrow A=A\) (luôn đúng với mọi \(x\in R\) )
31 tháng 7 2021
Ta có: \(A=\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}+\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}+\dfrac{x+1}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1+x-\sqrt{x}+1+x+1}{\sqrt{x}}\)
\(=\dfrac{3x+3}{\sqrt{x}}\)
Để A-|A|=0 thì A=|A|
\(\Leftrightarrow3x+3\ge0\)
hay \(x\ge-1\)
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
LL
1
N
23 tháng 11 2021
\(\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{x-2\sqrt{x}-x+2\sqrt{x}-\sqrt{x}+2-\sqrt{x}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{-2\sqrt{x}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{-2\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{-2}{\sqrt{x}-2}\)
CM
12 tháng 7 2017
x + 2 x - 3 = x - x + 3 x - 3 = x ( x - 1) + 3( x - 1) = ( x - 1)( x + 3)
a) Với điểu kiện x ≥ 0; x ≠ 1 ta có:
2 tháng 7 2021
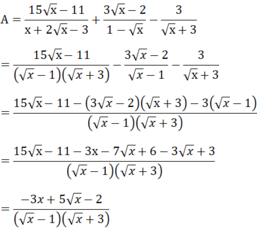
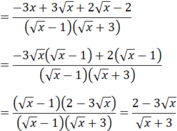
a, ĐKXĐ : \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
Ta có : \(A=\dfrac{1}{\sqrt{x}-1}-\dfrac{x-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x+\sqrt{x}+1-x+\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{2}{x+\sqrt{x}+1}\)
\(50< \frac{120}{x}< 70\)
\(\Rightarrow\frac{1}{50}>\frac{x}{120}>\frac{1}{70}\)
\(\Rightarrow\frac{120}{70}< x< \frac{120}{50}\)