Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A=\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}\)
\(\Rightarrow A< \frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{99\cdot100}\)
\(\Rightarrow A< \frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(\Rightarrow A< \frac{1}{2}-\frac{1}{100}< \frac{1}{2}\)
b) b = a - c => b + c = a
\(\left\{{}\begin{matrix}\frac{a}{b}\cdot\frac{a}{c}=\frac{a^2}{bc}\\\frac{a}{b}+\frac{a}{c}=\frac{ac+ab}{bc}=\frac{a\left(b+c\right)}{bc}=\frac{a^2}{bc}\end{matrix}\right.\)
\(\Rightarrow\frac{a}{b}\cdot\frac{a}{c}=\frac{a}{b}+\frac{a}{c}\)
Bước 2 bạn sai rồi. Vd: \(\frac{1}{3x3}\) đâu bằng hay nhỏ hơn \(\frac{1}{2x3}\)

Bài 1 :
\(A=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{50-49}{49.50}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{3}+...+\frac{1}{49}-\frac{1}{50}\)
\(=1-\frac{1}{50}< 1\left(1\right)\)
\(B=\frac{1}{10}+\left(\frac{1}{11}+\frac{1}{12}+...+\frac{1}{99}+\frac{1}{100}\right)\)\(>\frac{1}{10}+\frac{1}{100}.90=1\left(2\right)\)
Từ (1) và ( 2) ta có \(A< 1\) \(B>1\)NÊN \(A< B\)
Bài 2:
\(S=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\)
\(=\frac{\left(a+b+c\right)-\left(b+c\right)}{b+c}+\)\(\frac{\left(a+b+c\right)-\left(c+a\right)}{c+a}\)\(+\frac{\left(a+b+c\right)-\left(a+b\right)}{a+b}\)
\(=\frac{7-\left(b+c\right)}{b+c}+\frac{7-\left(c+a\right)}{c+a}+\frac{7-\left(a+b\right)}{a+b}\)
\(=7.\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right)-3\)
\(=7.\frac{7}{10}-3\)\(=\frac{49}{10}-3=\frac{19}{10}\)
\(S=\frac{19}{10}>\frac{19}{11}=1\frac{8}{11}\)
Chúc bạn học tốt ( -_- )
Bài 1:
ta có: \(A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{49.50}\)
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{49}-\frac{1}{50}\)
\(A=1-\frac{1}{50}< 1\)
\(\Rightarrow A< 1\)(1)
ta có: \(\frac{1}{11}>\frac{1}{100};\frac{1}{12}>\frac{1}{100};...;\frac{1}{99}>\frac{1}{100}\)
\(\Rightarrow\frac{1}{11}+\frac{1}{12}+...+\frac{1}{99}+\frac{1}{100}>\frac{1}{100}+\frac{1}{100}+...+\frac{1}{100}+\frac{1}{100}\) ( có 90 số 1/100)
\(=\frac{90}{100}=\frac{9}{10}\)
\(\Rightarrow B=\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+...+\frac{1}{99}+\frac{1}{100}>\frac{1}{10}+\frac{9}{10}=1\)
\(\Rightarrow B>1\)(2)
Từ (1);(2) => A<B

\(A=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\)
\(=\frac{a}{b+c}+1+\frac{b}{c+a}+1+\frac{c}{a+b}+1-3\)
\(=\frac{a+b+c}{b+c}+\frac{a+b+c}{c+a}+\frac{a+b+c}{a+b}-3\)
\(=\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right)-3\)
\(=7.\frac{7}{10}-3=\frac{49}{10}-3=\frac{19}{10}\)
Ta có:\(1\frac{8}{11}=\frac{19}{11}< \frac{19}{10}\left(đpcm\right)\)
V...

1. \(A=\frac{n+1}{n-2}=\frac{n-2+3}{n-2}=1+\frac{3}{n-2}\)
A nguyên nên \(3⋮n-2\). Vậy \(n-2\in\left(1,-1,3,-3\right)\Rightarrow n\in\left(3,1,5,-1\right)\)thì A nguyên.
2. a,Ta cần CM \(\frac{a}{b}< \frac{a+c}{b+c}\Rightarrow a\left(b+c\right)< b\left(a+c\right)\Rightarrow ab+ac< ab+bc\Rightarrow ac< bc\)(luôn đúng)
Suy ra điều phải chứng minh.
b, Có: \(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=\frac{a+b+c}{a+b+c}=1\)
Có:(suy ra từ phần a) \(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}< \frac{a+c}{a+b+c}+\frac{b+a}{a+b+c}+\frac{c+b}{a+b+c}=\frac{2\left(a+b+c\right)}{a+b+c}=2\)
Vậy \(1< \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}< 2\)
BẤM ĐÚNG CHO MÌNH, KO THÌ LẦN SAU KO GIÚP NỮA
Để \(A=\frac{n+1}{n-2}\)có giá trị nguyên => n + 1 chia hết cho n-2
\(=>\left(n-2\right)+3⋮\)\(n-2\)
Mà \(\left(n-2\right)⋮\)\(n-2\)
\(=>3⋮\)\(n-2\)
\(=>n-2\inƯ\left(3\right)=\){1;-1;3;-3}
Ta có bảng :
| n-2 | 1 | -1 | 3 | -3 |
| n | 3 | 1 | 5 | -1 |
Vậy \(n\in\){3;1;5;-1} để \(A=\frac{n+1}{n-2}\in Z\)

A = -4/5x(1/2+1/3+1/4)= -4/5x1 = -4/5
B = 6/19 x ( 3/4+4/3+-1/2)= 6/19x 19 = 6
C = 2002/2003x(3/4+5/6-19/12)=2003/2002x0=0

\(\frac{x-1}{6}=\frac{1}{6}\Leftrightarrow6\left(x-1\right)=6\Leftrightarrow6x-6=6\Leftrightarrow6x=12\Leftrightarrow x=2\)
\(\frac{x-2}{5}=\frac{8}{10}=\frac{4}{5}\Leftrightarrow5\left(x-2\right)=4.5=20\Leftrightarrow5x-10=20\Leftrightarrow5x=30\Leftrightarrow x=6\)
\(\frac{x-1}{8}=\frac{1}{2}\Leftrightarrow2\left(x-1\right)=8\Leftrightarrow2x-2=8\Leftrightarrow2x=10\Leftrightarrow x=5\)
\(\text{ câu 1 mk nghĩ là so sánh chứ nhỉ?}\)

\(\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\Rightarrow\frac{bc+ac}{abc}=\frac{ab}{abc}\Rightarrow bc+ac=ab\)
\(\Rightarrow ab-ac-bc=0\Rightarrow a\left(b-c\right)-c\left(b-c\right)=c^2\)
\(\Rightarrow\left(b-c\right)\left(a-c\right)=c^2\Rightarrow\frac{a-c}{c}=\frac{c}{b-c}\)

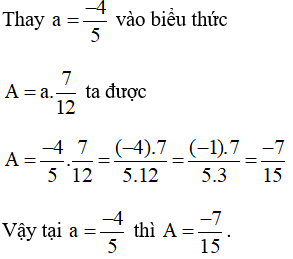



\(=\frac{1}{a^2}+\frac{2}{ab}+\frac{1}{b^2}+\frac{2}{bc}+\frac{1}{c^2}+\frac{2}{ac}\)
\(=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{2a+2b+2c}{abc}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\)
\(A=\frac{1}{a^2}+\frac{2}{ab}+\frac{1}{b^2}+\frac{2}{bc}+\frac{1}{c^2}+\frac{2}{ac}=\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2\)
Linh không biết a + b + c = 0 để làm gì?