Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giá trị tần suất của giá trị 5 là:
72 400 . 100 % = 18%
Chọn C

Ta có: fi = n i N . 100 % suy ra ni= f i . N 100 %
Do đó; tần số xi =9 là: 2 % . 500 100 % = 10
Chọn A

50%=1/2
Phân số tương ứng với 12 bài là:
1-1/2-2/5=1/10(số bài)
Số bài của trường đó là:
12:1/10=120(bài)
Vậy trường đó có 120 bài kiểm tra tương đương với 120 HS
ĐS:120 học sinh
Đổi: \(50\%=\frac{1}{2}\)
Phân số ứng với 12 bài loại trung bình là:
\(1-\left(\frac{1}{2}+\frac{2}{5}\right)=\frac{1}{10}\)
Số học sinh khối 6 của trường đó là:
\(12:\frac{1}{10}=120\) (học sinh)
Đáp số:\(120\) học sinh

Xét trong 34 học sinh có ít nhất 1 môn đạt điểm 10
Gọi A, B, C lần lượt là tập hợp học sinh đạt điểm 10 của các môn Toán, Lý, Hóa, gọi D là tập hợp học sinh đạt điểm 10 đúng hai trong 3 môn
\(\Rightarrow\left|A\right|=23;\left|B\right|=20;\left|C\right|=21\)
\(\left|A\cap B\cap C\right|=5\)
Ta có:
\(\left|A\cup B\cup C\right|=\left|A\right|+\left|B\right|+\left|C\right|-2\left|A\cap B\cap C\right|-\left|D\right|\)
\(\Rightarrow34=23+20+21-2.5-\left|D\right|\)
\(\Rightarrow D=20\)
Số bạn chỉ đạt điểm 10 một hoặc hai môn là:
41-5-7=29(bạn)
Gọi x(bạn) là số bạn đạt điểm 10 đúng hai môn, gọi A,B,C lần lượt là tập hợp số bạn đạt điểm 10 ở các môn Toán,Lý,Hóa
Theo đề, ta có: n(A)=23; n(B)=20; n(C)=21, \(n\left(A\cap B\cap C\right)=5;n\left(A\cup B\cup C\right)=41\)
Ta có: \(n\left(A\cup B\cup C\right)=n\left(A\right)+n\left(B\right)+n\left(C\right)-2\cdot n\left(A\cap B\cap C\right)-x\)
=>41=23+20+21-2*5-x
=>x=13

Do M thuộc d nên tọa độ M có dạng: \(M\left(2y-3;y\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(4-2y;3-y\right)\\\overrightarrow{MB}=\left(1-2y;4-y\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}=\left(5-4y;7-2y\right)\)
\(T=\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\sqrt{\left(5-4y\right)^2+\left(7-2y\right)^2}\)
\(T=\sqrt{20y^2-68y+74}=\sqrt{20\left(y-\frac{17}{10}\right)^2+\frac{81}{5}}\ge\sqrt{\frac{81}{5}}\)
Dấu "=" xảy ra khi \(y=\frac{17}{10}\Rightarrow x=\frac{2}{5}\Rightarrow x+2y=\frac{19}{5}\)
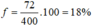
Đáp án B.
Tần số n = f . N = 5 % . 420 = 21