Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ở quỹ đạo L là F thì ở K sẽ là 4F => ở N sẽ là 4F/\(^{4^2}\) = F/4

+ Bán kính quỹ đạo dừng của electron theo mẫu nguyên tử Bo: rn = n2r0.
→ Lực tương tác tĩnh điện giữa electron và hạt nhân theo định luật Culong tỉ lệ nghịch với bình phương khoảng cách
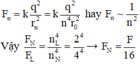
ü Đáp án A

+ Bán kính quỹ đạo dừng của electron theo mẫu nguyên tử Bo: rn = n2r0.
→ Lực tương tác tĩnh điện giữa electron và hạt nhân theo định luật Culong tỉ lệ nghịch với bình phương khoảng cách
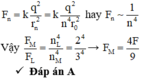

Năng lượng của nguyên tử ở trạng thái dừng \(n\):
\(E_n =-\frac{13,6}{n^2}.(eV)\)
Electron nhảy từ P (n=6) về K (n=1): \(hf_1 = E_6-E_1.(1)\)
Electron nhảy từ P (n=6) về L (n=2): \(hf_2 = E_6-E_2.(2)\)
Electron nhảy từ L (n=2) về K (n=1): \(hf_6 = E_2-E_1.(3)\)
Lấy (1) trừ đi (2), so sánh với (3) ta được : \(hf_1 -hf_2 = hf_3\)
=> \(f_3=f_1 -f_2.\)

Năng lượng của electron ở trạng thái dừng n là \(E_n = -\frac{13,6}{n^2}.(eV)\)
\(hf_1 =\frac{hc}{\lambda_1}= E_3-E_1.(1) \)
\(hf_2 =\frac{hc}{\lambda_2}= E_5-E_2.(2) \)
Chia hai phương trình (1) và (2): \(\frac{\lambda_2}{\lambda_1}= \frac{E_3-E_1}{E_5-E_2}.(3)\)
Mặt khác: \(E_3-E_1 = 13,6.(1-\frac{1}{9}).\)
\(E_5-E_2 = 13,6.(\frac{1}{4}-\frac{1}{25}).\)
Thay vào (3) => \(\frac{\lambda_2}{\lambda_1}= \frac{800}{189}\) hay \(189 \lambda_2 = 800 \lambda_1.\)

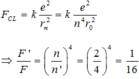
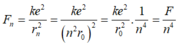
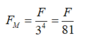
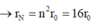
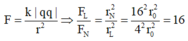
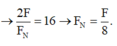
Đáp án A
Ta có:
Qũy đạo dừng L ứng với n = 2, quỹ đạo N ứng với n = 4
Do đó: